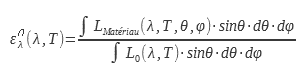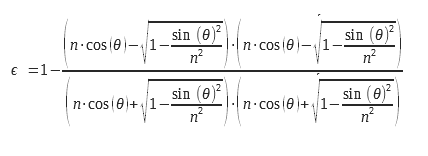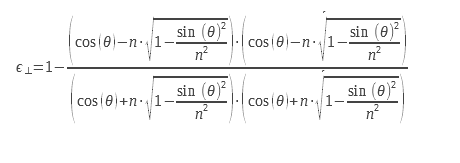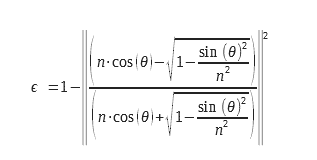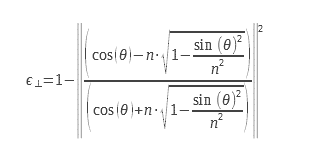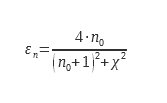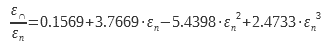Medición de la emisividad térmica

1. 1 Diferentes grados de emisión

Las superficies de los materiales pueden intercambiar energía en forma de radiación. La cantidad de energía que puede emitir una superficie depende de su temperatura y de sus propiedades. La ley de radiación de Planck indica la luminancia espectral de energía para una superficie teórica denominada cuerpo negro :

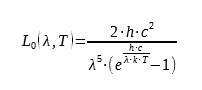
donde h = 6,62617·10−34 Js es la constante de Planck, c es la velocidad de la luz en el medio considerado (tomamos el valor de c en el vacío: c = 299792458 m·s−1) y k = 1,38066·10−23 JK−1 es la constante de Boltzmann. La luminancia espectral L0 se expresa en Wm-3.sr-1.

Para un material determinado, esta luminancia se pondera con un coeficiente entre 0 y 1 y se denomina emisividad. La escribimos con ε.

Este coeficiente puede depender de la longitud de onda, el ángulo de incidencia y la temperatura: ε(λ,T,θ,φ).
Los grados de emisión se clasifican según las áreas espaciales y espectrales de la radiación. Denominamos emisividad total a la emisividad calculada para todo el espectro y emisividad monocromática a la emisividad calculada para una sola longitud de onda. Denominamos emisividad hemisférica a la emisividad calculada para todas las direcciones y emisividad direccional a la emisividad calculada en una dirección.

1.1 Emisividad monocromática dependiente de la dirección

La emisividad monocromática dependiente de la dirección ε_λ^| es la relación entre la luminancia del material y la de un cuerpo negro para una dirección y longitud de onda determinadas. Es la magnitud que permite la descripción más precisa de un material determinado :

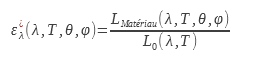
L0 es independiente de la dirección de incidencia para un cuerpo negro.
La mayoría de los materiales tienen una emisividad que no depende de la orientación y, por lo tanto, tampoco de ϕ.
En superficies lisas, esta emisividad puede depender de la polarización de la luz.

1.2 Emisividad monocromática hemisférica

La emisividad monocromática hemisférica es la relación entre la densidad de potencia superficial irradiada por la superficie del material examinado y la densidad de potencia superficial irradiada por un cuerpo negro para una longitud de onda determinada :

1.3 Emisividad total

La emisividad total es la relación entre la luminancia emitida por la superficie del material examinado y la luminancia emitida por un cuerpo negro en todo el espectro electromagnético :

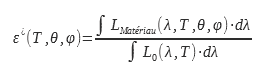
Este valor de emisividad es de interés para los usuarios de cámaras termográficas. Permite relacionar la luminancia en una dirección con la temperatura. Este cálculo o medición de la emisividad puede realizarse en un rango de longitudes de onda idéntico al de la cámara o en un rango espectral específico :

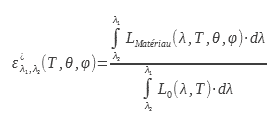
1.4 Emisividad total

La emisividad total ε es la relación entre la emisividad total del material y la de un cuerpo negro para todas las longitudes de onda a una temperatura determinada :

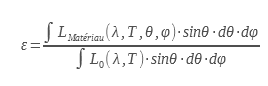
Esta emisividad es interesante para los térmicos a la hora de calcular el balance térmico de paredes opacas. Permite calcular el intercambio de radiación de una superficie que ha sido llevada a la temperatura T.

1.5 Casos especiales

Si la emisividad de un material no depende de la longitud de onda, se denomina cuerpo gris. Esta propiedad no se da en la realidad, por lo que denominamos cuerpo gris a un cuerpo cuya emisividad no varía en el rango espectral estudiado. Un cuerpo gris cuyas propiedades espectrales no varían en función de la temperatura tiene una emisividad que tampoco varía en función de la temperatura. Por el contrario, una superficie con una emisividad espectral que cambia con la longitud de onda tiene una emisividad total que cambia con la temperatura, ya que el espectro de radiación de un cuerpo negro cambia con la temperatura.

Como acabamos de ver, la emisividad de un material real también depende generalmente del ángulo de emisión. Por lo tanto, no se trata de una superficie de Lambert. Sin embargo, en los dieléctricos, la emisividad solo cambia ligeramente en un amplio rango de ángulos (de 0 a 60◦). En este rango angular, se consideran superficies de Lambert. La figura 1 de (1) muestra la emisividad direccional total en función del ángulo para una serie de materiales. Podemos ver que no varía hasta un ángulo de 60◦. Además, la ley de variación de la emisividad en función del ángulo muestra una similitud en la forma.

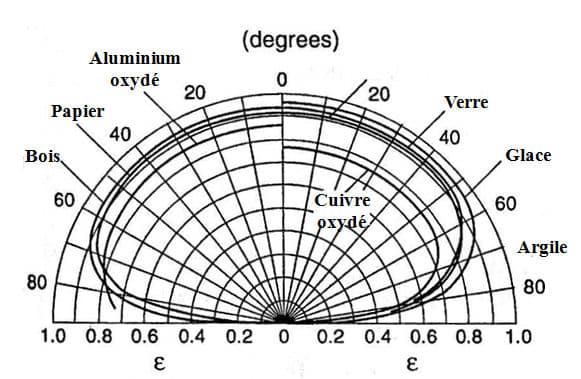
Figura 1

Emissionismo total en función de la dirección a partir de (1)

2. Cálculo de la emisividad a partir del índice complejo

En el caso de la radiación electromagnética, la ley de conservación de la energía se expresa mediante la ley de Kirchhoff. En general, esta ley relaciona, para una longitud de onda determinada, el factor de transmisión, el factor de reflexión hemisférica direccional y la absorción, que en este caso es igual a la emisividad.

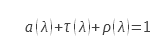
Aquí, a es el factor de absorción espectral, τ es el factor de transmisión espectral y ρ es el factor de reflexión direccional hemisférica.
Para un material opaco, esta relación es

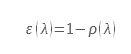
Dado que ε = a y, para un material opaco, τ = 0.

La ecuación (8) es la base de todos los métodos indirectos para medir la emisividad. También permite calcular la emisividad a partir del propio factor de reflexión, que se calcula según las relaciones de Fresnel. Este enfoque solo es válido para dióptricos, es decir, para superficies lisas.

1.6 Cálculo de la emisividad para las dos polarizaciones de la luz

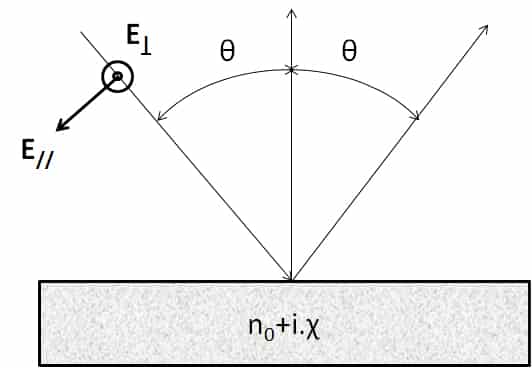
Para la dioptría plana, la emisividad se puede calcular a partir de la expresión de los coeficientes de reflexión, que se calculan a partir del índice complejo n = n0+ i. χ. Este cálculo detallado se encuentra en (2) de las ecuaciones de Maxwell. Estas expresiones se derivan de los coeficientes de Fresnel para la reflexión y se encuentran en (3). Las ecuaciones 9 y 10 pueden utilizarse con índices complejos, lo que permite utilizarlas para calcular la emisividad de los metales. Las consideraciones sobre las condiciones límite en el plano de la dioptría hacen necesario calcular un coeficiente de reflexión y, por lo tanto, una emisividad para dos polarizaciones diferentes. Estas polarizaciones se explican en la figura de la figura 2.

Figura 2

Reflejo especular en una dioptría plana

Para la luz no polarizada, debemos calcular la media aritmética de los dos grados de emisión correspondientes a las dos polarizaciones. Las expresiones de los dos grados de emisión para las dos polarizaciones se indican a continuación:

Podemos escribirla de otra forma:

También podemos calcular la emisividad direccional normal ε_n. En este caso, las dos polarizaciones son equivalentes y obtenemos el siguiente resultado para un índice complejo n :

1.7 Caso de dieléctricos

La figura 3 de (2) muestra la emisividad direccional en función del ángulo para un dieléctrico con un índice de refracción de 1,5: Esto corresponde a una permitividad dieléctrica relativa de 2,25:

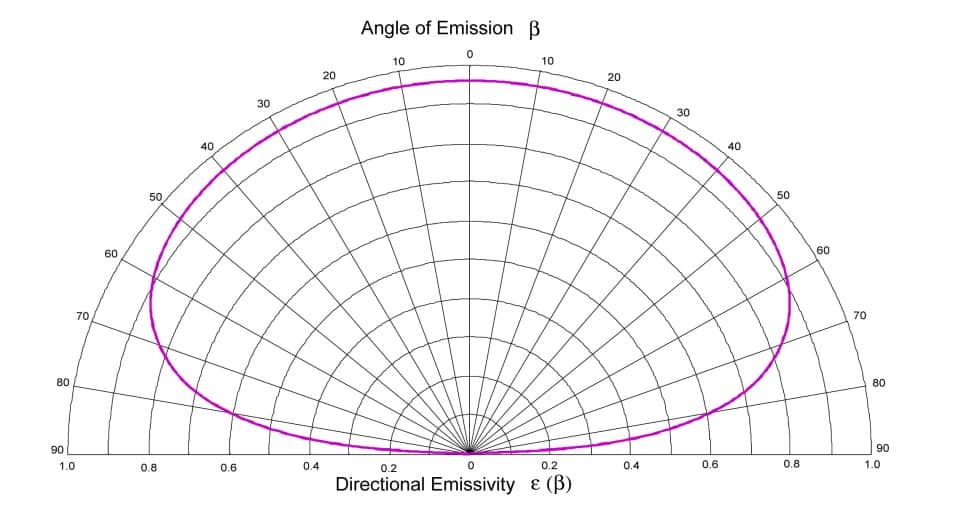
Figura 3

Emisividad dependiente de la dirección en función del ángulo para un dieléctrico con un índice de refracción de 1,5 (2)

Estas son las propiedades típicas del vidrio a base de borosilicato. Observamos que, en teoría, encontramos el mismo indicador de emisividad que el medido experimentalmente (figura 1). Dado que el único parámetro que puede modificar la emisividad de un dióptrico dieléctrico liso es el índice de refracción real, siempre tenemos el mismo indicador de emisividad para un índice de refracción dado. Por lo tanto, se puede calcular la emisividad hemisférica mediante la integración de todo el hemisferio.

Por lo tanto, la relación entre la emisividad hemisférica y la emisividad direccional normal es solo una función del índice de refracción y, por lo tanto, solo de la emisividad direccional normal (figura 1). Por lo tanto, podemos derivar la emisividad hemisférica a partir de la emisividad direccional normal y viceversa. Estos informes se recogen en forma de tabla en la norma NF EN 12898 para determinar la emisividad del vidrio de construcción. Este estudio puede utilizarse para un dieléctrico no liso con una buena aproximación. De hecho, la rugosidad solo tiene una influencia muy pequeña en el indicador de emisividad de un dieléctrico. Estas consideraciones se abordan en la sección 2.4.

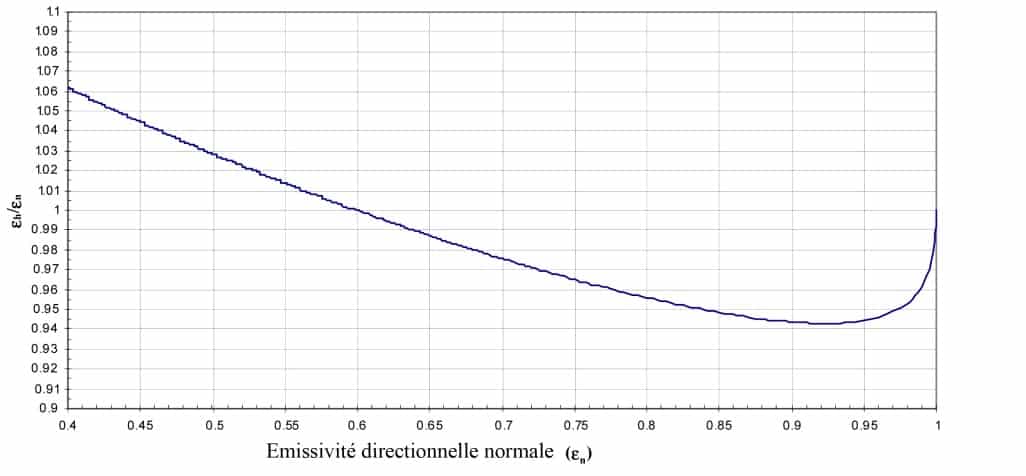
Figura 4

Relación entre la emisividad del hemisferio y la emisividad en dirección normal en función de la emisividad en dirección normal para dieléctricos lisos (2)

1.8 Caso de metales y conductores

De la misma manera, podemos representar el indicador de emisividad para un dióptrico aire/metal. El resultado es un indicador de emisividad teórico similar al que se puede determinar para un metal como el aluminio. El valor representado en la figura 5 de (2) se calculó para un índice de refracción típico de metales como el aluminio: n = 5,7 + 9,7i. La correspondencia entre la emisividad hemisférica y la emisividad direccional normal también existe para los conductores, pero el indicador de emisividad es diferente.

Por lo tanto, es necesario tratar los conductores por separado de los dieléctricos para determinar la relación entre las dos emisividades. Este estudio no puede aplicarse a conductores no lisos. De hecho, la rugosidad tiene una fuerte influencia en el indicador de emisividad de un metal, ya que la emisividad de un metal depende en gran medida de su rugosidad. En [30] se puede encontrar un estudio más detallado sobre la emisividad de los metales en función de la rugosidad.

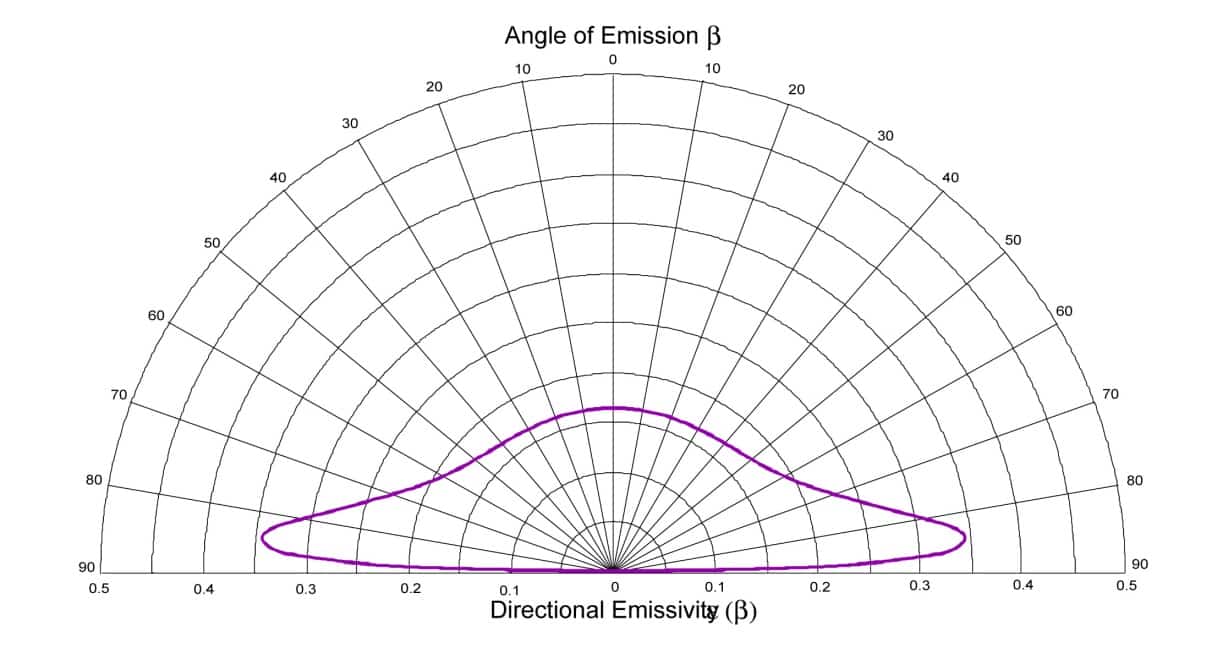
Figura 5

Emisividad dependiente de la dirección en función del ángulo para un metal con un índice de refracción de n = 5,7 + 9,7. i

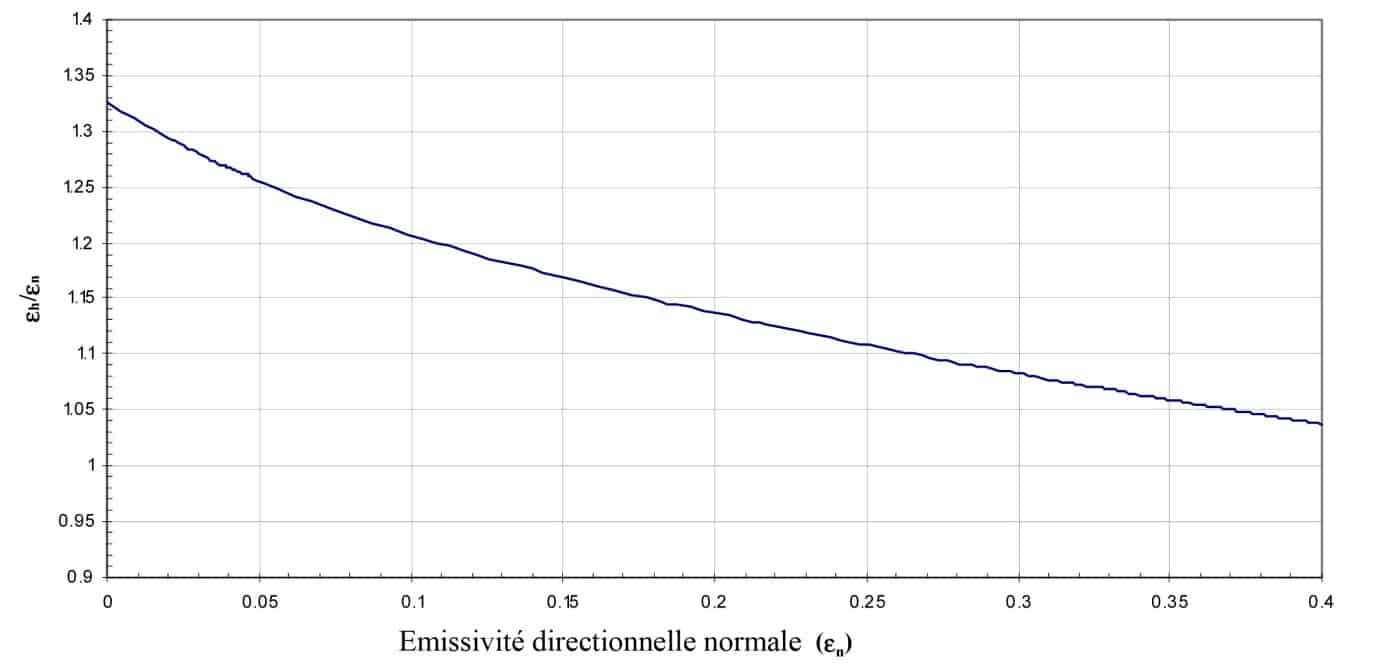
Figura 6.

Relación entre la emisividad hemisférica y la emisividad direccional normal en función de la emisividad direccional normal para conductores lisos. (2)

En los conductores pueden variar dos parámetros, n0 y χ. La figura 6 muestra una curva teórica obtenida mediante la variación de la parte imaginaria del índice. Para casos más complejos y, en particular, para superficies rugosas, los estudios experimentales han permitido la creación de valores tabulares.

1.9 Relación entre la emisividad direccional normal y la emisividad hemisférica

Por razones de simplicidad, la emisividad direccional se mide a menudo con una incidencia casi normal. Sin embargo, a menudo es necesario determinar la emisividad hemisférica.

Se trata de la integración de la emisividad direccional en todos los ángulos espaciales utilizables. Si no es posible medirla en todo el rango de incidencia, debe ser posible deducir la emisividad hemisférica a partir de la emisividad direccional con incidencia casi normal. Este cálculo es teóricamente posible para dióptricos lisos de dieléctricos, ya que la emisividad solo depende del índice normal (figura 1). Los valores de la tabla 1 proceden de la norma ISO 12898. Está prevista para la medición de la emisividad de acristalamientos.

Tabla 1 Factores para calcular la emisividad hemisférica total a partir de εn para una superficie dieléctrica lisa

Algunos estudios destacados han permitido documentar este coeficiente ε∩/ εn. Para superficies lisas con baja emisividad (típicamente metales), Rubin y Hartmann (4) utilizaron plata e Inlayers2O3 sobre vidrio. Utilizando datos experimentales y las relaciones de Kramer-Kroning, se obtuvo una expresión analítica

Para dieléctricos cuya emisividad εn está entre 0,68 y 0,98, se usa otra expresión (4) (5):

Estos datos se resumieron y completaron en dos informes de investigación europeos (6) (7). Permitieron proporcionar los datos necesarios para la elaboración de la norma ISO 12898.
Estos datos se muestran en la figura 7. La curva «Metales» corresponde a la ecuación (14) y la curva «Dieléctricos» a la ecuación (15). Los valores que figuran en la tabla de la norma ISO 13898 también se muestran en este diagrama.

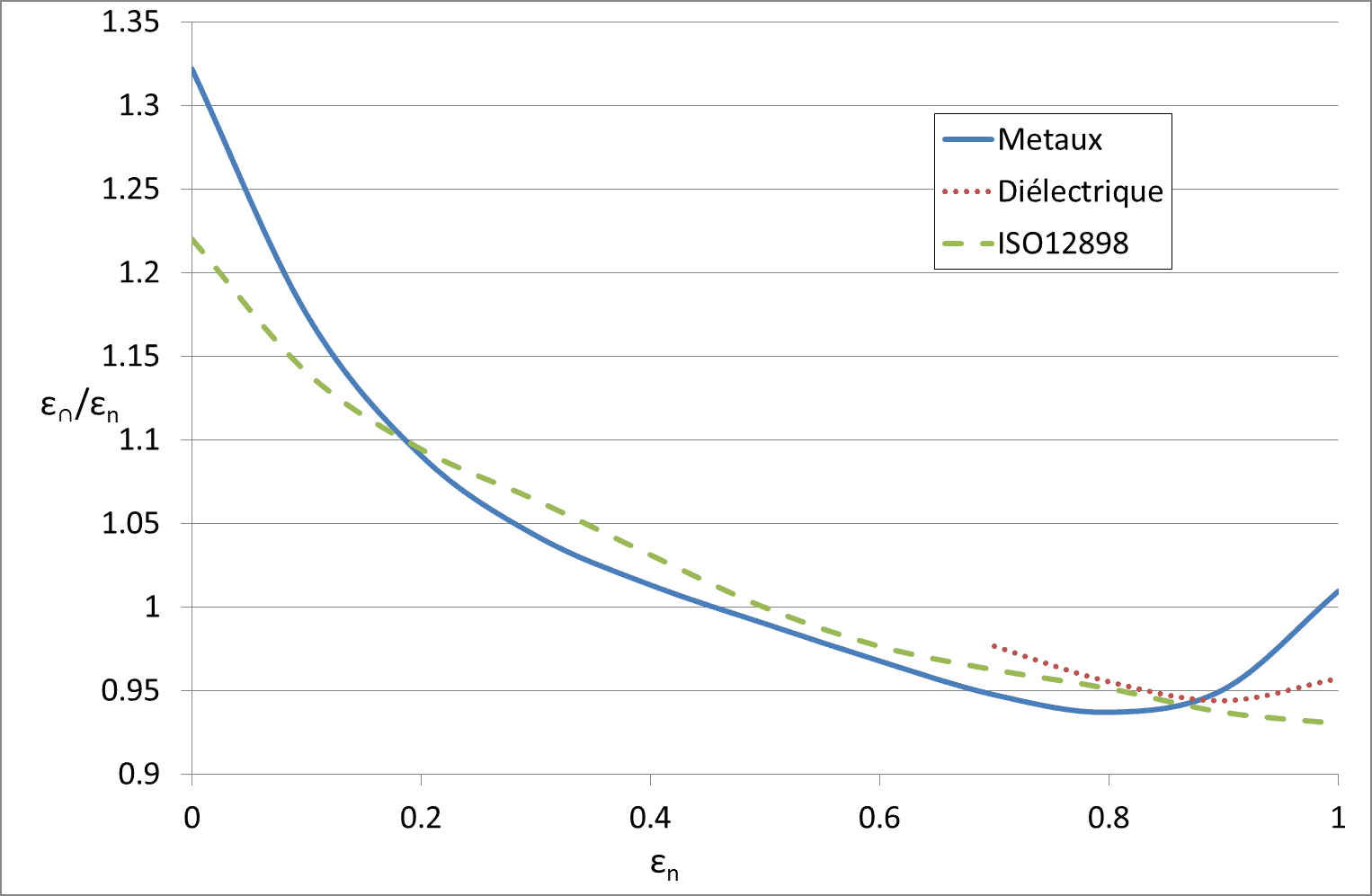
Figura 7

Relación entre ε y εn según las diferentes fuentes

3 Los diferentes métodos para medir la emisividad térmica

1.10 Clasificación de los métodos

En este capítulo se tratan los métodos para medir la emisividad. Se han clasificado según el principio físico de medición. Hemos separado los denominados métodos directos de los denominados métodos indirectos. Los métodos directos son aquellos en los que se mide directamente la potencia irradiada por la superficie: se trata de métodos calorimétricos y radiométricos.
Los métodos indirectos son aquellos en los que las propiedades de las superficies en el rango espectral infrarrojo se derivan de las propiedades ópticas mediante reflectometría: este es el caso de todos los demás métodos. Todos los dispositivos comerciales utilizan estos métodos indirectos de una forma u otra. Los métodos directos solo están limitados por el equipo de prueba utilizado. Los métodos indirectos adolecen de distorsiones intrínsecas en el propio método de medición.

1.11 Método calorimétrico

Este método permite evaluar las transferencias de radiación sin descuidar determinados ángulos de incidencia o longitudes de onda. Consiste en elaborar un balance energético de las pérdidas por radiación de la muestra analizada, cuando solo estas pérdidas son relevantes. Se trata de un método directo y absoluto, es decir, no se necesita un estándar de referencia para la emisividad para
determinar la emisividad de la muestra. Sin embargo, este método sigue siendo costoso. Para eliminar las transferencias por conducción térmica y convección, la muestra debe colocarse en una atmósfera reducida (normalmente 10−5 mbar). La muestra se calienta y se mantiene a la temperatura a la que se desea determinar la emisividad. Para mantener su temperatura, debe recibir energía :

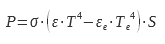
donde P es la potencia emitida por la muestra, ε es su emisividad, σ es la constante de Stefan-Boltzmann, T es la temperatura de la muestra, εe es la emisividad de la carcasa, Te es la temperatura de la carcasa y S es la superficie de emisión de la muestra. La potencia necesaria para mantener la muestra a la temperatura a la que se va a determinar la emisividad se suministra eléctricamente en forma de efecto Joule. La figura 8 muestra esquemáticamente un dispositivo para medir la emisividad según el método calorimétrico. La carcasa (F) se mantiene al vacío mediante un dispositivo de bombeo conectado a la carcasa a través de la tubería A.

Los cables de alimentación y medición (B) están conectados a la muestra a través de un bloque de conexión C. Este sirve como protección para evitar pérdidas por conducción térmica. La temperatura de este bloque de conexión se mantiene y se regula a la misma temperatura que la muestra. De este modo, la potencia disipada por conducción térmica a través de los cables de alimentación y medición entre el bloque de conexión y la muestra es igual a cero debido a la ausencia de gradiente de temperatura. El disco de muestra con superficie de radiación conocida está suspendido en la envoltura. La envoltura E es un criostato térmicamente aislado, que suele estar lleno de nitrógeno líquido. Se utiliza helio cuando se deben medir los grados de emisión a bajas temperaturas (por debajo de 250 K) para la industria aeroespacial. En (8) se describe un dispositivo de este tipo. El interior de la carcasa F está recubierto con un revestimiento de alto grado de emisión y emisividad espectral, que varía muy poco con la longitud de onda. La elección de la temperatura del criostato depende de la necesidad de que ε.T4 ≫ εe.Te4. La temperatura ideal debería permitir una polarización mucho menor que la incertidumbre de medición del dispositivo. A partir de la relación 16 podemos deducir la emisividad :

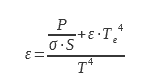
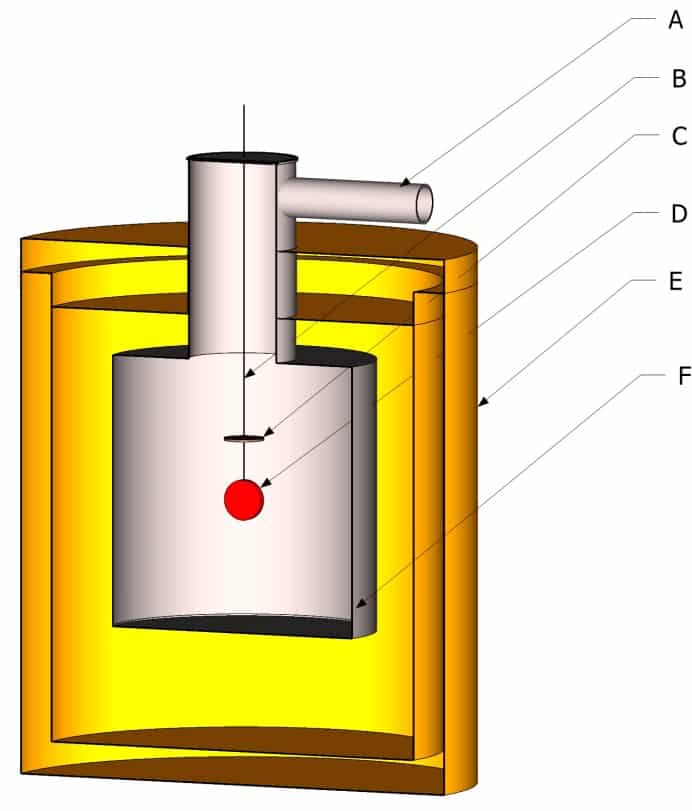
Figura 8

Representación esquemática del método calorimétrico

El método calorimétrico es el único que permite determinar directamente la emisividad hemisférica total. Para ello se tiene en cuenta toda la radiación. Dado que no requiere ninguna referencia ni estándar de emisividad, se considera el método de referencia. Sin embargo, este método sigue siendo complicado y lento de aplicar. Sería difícil crear una base de datos de emisividad utilizando únicamente este método.

La mayor incertidumbre radica en la medición de la temperatura superficial. Esta puede extrapolarse midiendo el gradiente de temperatura en el interior de la muestra con diferentes sensores (9). Además, las muestras deben calibrarse en cuanto a su tamaño para que quepan en el medidor. En (10) se describen otros dispositivos más sencillos.

1.12 Método radiométrico

1.1.1 Método mediante medición directa del flujo/luminancia

Este método consiste en comparar la luminancia de una muestra con la de un cuerpo negro calentado a la misma temperatura. El dispositivo se muestra en la figura 9. En esta figura, la muestra A se calienta a la temperatura a la que se va a medir la emisividad. Esta se coloca en una cámara refrigerada B con las mismas condiciones de temperatura que en el método calorimétrico (ε.T4 ≫ εe.Te4). Un cuerpo negro E calentado a la misma temperatura que la muestra sirve como referencia de luminancia. La luminancia del cuerpo negro y la de la muestra se miden sucesivamente con ayuda del espejo basculante C. La relación entre estas dos luminancias da como resultado el grado de emisión. El cuerpo negro se coloca en una carcasa aislada sin condiciones de temperatura. Es posible realizar la medición con un cuerpo negro cuya temperatura difiera de la de la muestra. En este caso, se aplica una relación entre las temperaturas con la potencia 4.

Las dos luminancias se miden con el detector D. Puede tratarse de un detector infrarrojo de banda ancha (como una columna térmica) para medir la emisividad total. Este detector puede equiparse con una rueda de filtros para medir la emisividad espectral para diferentes longitudes de onda (11). Los dispositivos para medir la emisividad mediante comparación con un cuerpo negro del NIST (Instituto Nacional de Estándares y Tecnología, Gaithersburg, Maryland, Estados Unidos) se presentan en (12). En este dispositivo no hay ningún espejo basculante, el sistema de detección se mueve mediante un carro delante de las superficies que se van a medir y los cuerpos negros de referencia. Este dispositivo es una referencia en el campo de las mediciones de emisividad para temperaturas de 600 K a 1400 K. El medidor de emisividad descrito en (13) utiliza un espectrómetro infrarrojo de transformada de Fourier. Por lo tanto, la luminancia solo se mide en una dirección, es decir, se mide una emisividad direccional. Para medir diferentes ángulos de incidencia y volver a la emisividad hemisférica, algunos dispositivos permiten girar la muestra: este es el caso del dispositivo descrito en (13). El espectrómetro también puede sustituirse por un monocromador, como el dispositivo descrito en (14).

La medición radiométrica a temperatura ambiente requiere colocar la muestra en un criostato a muy baja temperatura y al vacío para evitar la condensación. En (15) se describe un dispositivo original que evita este problema. El principio sigue siendo el mismo, pero las mediciones se realizan a temperatura ambiente y el flujo medido se corrige a partir de las mediciones de temperatura de la carcasa y del chopper. Esto simplifica considerablemente el dispositivo, pero introduce fuentes de incertidumbre adicionales.

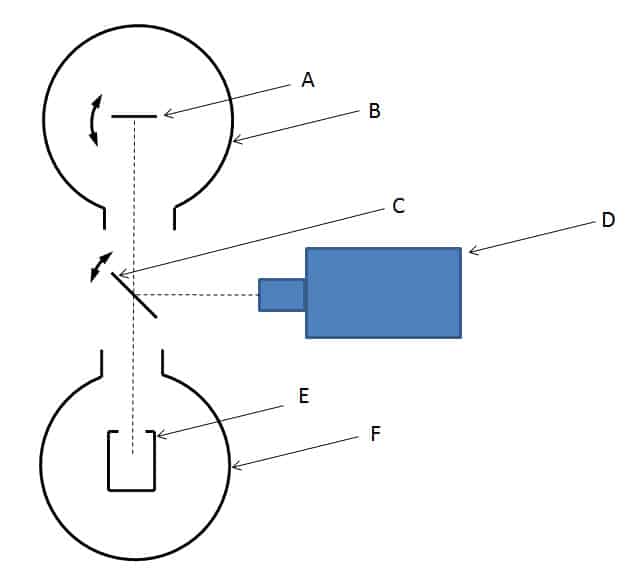
Figura 9

Método radiométrico

El procedimiento consiste en modular ligeramente la temperatura de la muestra en torno a la temperatura a la que se desea determinar la emisividad. De este modo, podemos separar el flujo reflejado del flujo propio de la muestra. Este es el principio del método radiométrico modulado.

Para determinar la emisividad, es necesario comparar el flujo medido con el de una superficie de emisividad conocida. Otro método consiste en modular adicionalmente una fuente hemisférica con una frecuencia diferente a la frecuencia de modulación de la muestra. Mediante la medición en dos muestras desconocidas, se pueden determinar los valores de emisividad y reflectividad. Con este método no se necesita una referencia de emisividad para la medición. El método radiométrico periódico se describe detalladamente en [20].

1.13 Métodos reflectométricos

El método reflectométrico consiste en medir el coeficiente de reflexión direccional hemisférica ρ^(∩ |) o el coeficiente de reflexión direccional hemisférica ρ^(| ∩ in) para calcular la emisividad direccional para una dirección que corresponde a la dirección utilizada para medir el coeficiente de reflexión. Este cálculo se basa en la ley de Kirchhoff (2). Esta ley se puede formular de la siguiente manera: para una superficie opaca que se encuentra en equilibrio térmico con su entorno, se aplica lo siguiente para una longitud de onda λ :

El equilibrio térmico implica una temperatura idéntica para el entorno y la superficie en cuestión. Esta relación puede extenderse a un rango de longitudes de onda.

Este coeficiente de reflexión se puede calcular midiendo la reflexión para todas las longitudes de onda y realizando la integración, ponderada con la emisividad del cuerpo negro, o asegurándose de que la reflexión se mida con una fuente de luz que tenga la misma distribución espectral de energía que el cuerpo negro a la temperatura considerada. También hay que asegurarse de que el detector de infrarrojos utilizado tenga una sensibilidad suficientemente constante en el rango espectral considerado. Si la reflexión espectral no varía con la temperatura, se puede calcular esta reflexión sin tener en cuenta la temperatura de la muestra. Veremos varios métodos para medir la emisividad a partir de la medición de la reflexión.

Figura 10

Representación esquemática de un dispositivo para medir la reflexión direccional hemisférica utilizando el método de la esfera de Ulbricht.

1.1.3 Método de la esfera integral

La figura 10 muestra el funcionamiento de una esfera integral. Esta debe estar provista en su interior de un revestimiento reflectante y difusor. La muestra se ilumina con una fuente de infrarrojos en una dirección determinada cercana a la normal. El ángulo de incidencia en las esferas integradoras comerciales oscila entre 8 y 12 grados. Tan pronto como la luz alcanza la muestra, se dispersa en todas las direcciones según el grado de reflexión del material. Tras varios reflejos, la luz llega al detector situado en el lateral. De este modo, el detector mide teóricamente casi todo el flujo luminoso reflejado por la muestra.

Un sistema de diafragma impide que el detector vea directamente la muestra, para no interferir en la medición. Se puede colocar un detector simétricamente respecto a la fuente para medir el reflejo especular. Esto es opcional y, en determinadas esferas, se puede colocar en el punto de reflexión especular una parte de la superficie difusa del mismo tipo que la esfera o dejarlo abierto. En el primer caso se mide todo el flujo luminoso reflejado (difuso y especular), en el segundo solo el flujo luminoso difuso.

Mediante sustracción se puede determinar el coeficiente de reflexión especular. Para realizar una medición del coeficiente de reflexión, el dispositivo debe calibrarse con una referencia de reflexión. Se utiliza el mismo tipo de recubrimiento que para la esfera. Por lo general, se trata de una superficie metálica pulida recubierta con una capa de oro. El NIST utiliza un dispositivo de este tipo. Se describe en (16).

1.1.4 Método utilizando una fuente modulada

Hasta ahora, con el método radiométrico, si queríamos medir el flujo emitido por la superficie, teníamos que eliminar el flujo del entorno radiante alrededor de la muestra. Por lo tanto, esta se colocaba en una envoltura enfriada a una temperatura Te para garantizar que σ.T4>> σ.Te4. Sin embargo, esta condición restrictiva es fácil de cumplir gracias a una carcasa refrigerada por agua para temperaturas de muestra del orden de 1000 K. No obstante, si se desea medir la emisividad a temperatura ambiente, la carcasa debe enfriarse a temperaturas criogénicas. Para evitar esta complejidad adicional, se puede modular la temperatura de la muestra que se va a medir en torno a la temperatura a la que se desea la emisividad (17). En este caso, se registra el flujo emitido modulado y se compara con una amplitud de modulación equivalente a la emitida por una superficie de referencia. Si no es posible modular la temperatura de la muestra, se puede utilizar un método reflectométrico y se puede modular el flujo utilizado para medir el factor de reflexión. Estos métodos se describen en (18) y se puede encontrar un ejemplo de aplicación concreto en (19).

Para separar el flujo propio de la muestra del flujo reflejado, se envía un flujo hemisférico modulado en frecuencia por encima de ella. El principio consiste en generar un flujo infrarrojo hemisférico que se modula alrededor de la muestra examinada y medir en una dirección el flujo reflejado por la superficie del material con una columna térmica. El diagrama de la figura 11 muestra el principio del dispositivo. El dispositivo se calibra previamente con un material de referencia conocido. La figura 12 muestra el esquema del dispositivo desarrollado por CERTES (19), así como una fotografía del instrumento. La cavidad consiste en un cubo de aluminio hueco abierto por la parte inferior. La temperatura de las paredes se modula con elementos Peltier. La medición del flujo reflejado se realiza a través de una abertura en la parte superior del dispositivo mediante una columna térmica equipada con una lente KRS5.

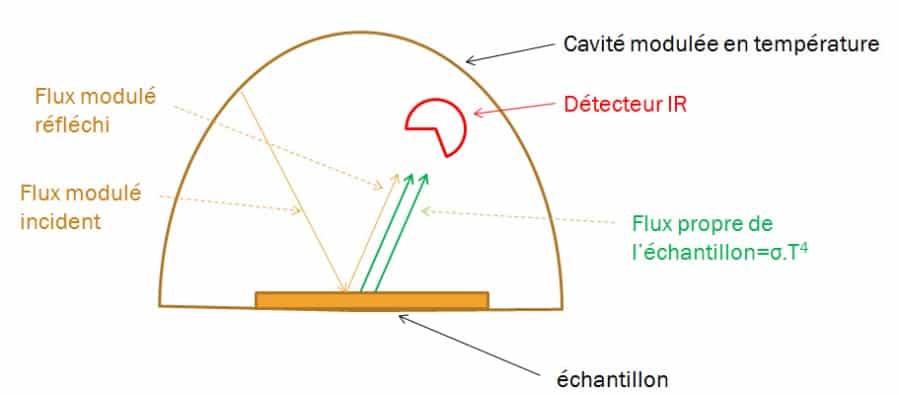
Figura 11

Principio del método de medición reflectométrico con una fuente modulada

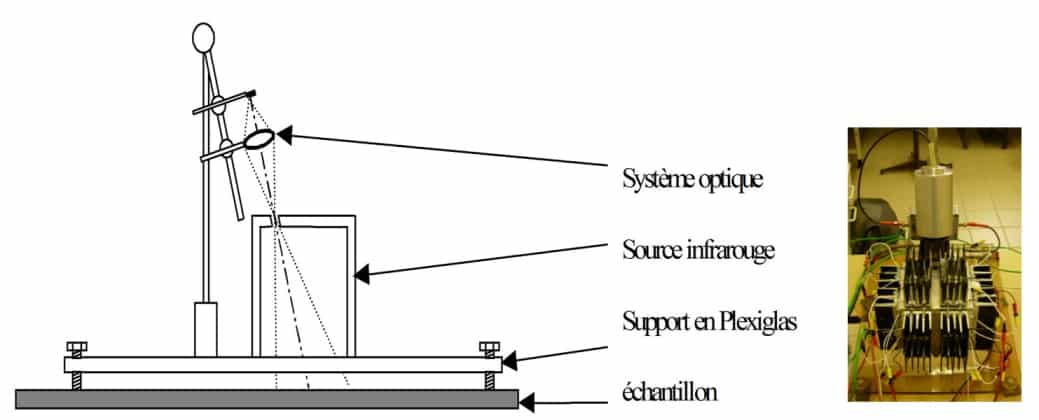
Figura 12

Diagrama y fotografía del medidor desarrollado por CERTES.

Otro método para modular el flujo hemisférico es el uso de un chopper tridimensional. Este dispositivo ha sido patentado por la Universidad París XII. A continuación se presenta el dispositivo.

EM3 de THEMACS Engineering:

El principio de este dispositivo es el mismo que el descrito anteriormente. Consiste en modular una fuente de radiación hemisférica mediante válvulas móviles. De este modo se evita la modulación de la cavidad térmica, que es muy lenta. El diagrama de la figura 21 muestra el principio de modulación.
La fuente es el cilindro B, que se calienta a una temperatura ligeramente superior a la temperatura ambiente. El cilindro móvil C y el diafragma fijo D ocultan la fuente hemisférica con una frecuencia de 10 Hz para la pared cilíndrica (6 ventanas) y de 5 Hz para la parte superior (3 ventanas). De esta manera, es posible distinguir un material reflectante de un material dispersante. Una columna térmica mide el flujo incidente y otra mide el flujo reflejado. La relación del flujo reflejado no depende de la intensidad emitida por la fuente.

Este emisímetro debe calibrarse previamente con dos superficies de emisividad conocida. Por lo general, utilizamos una superficie con una emisividad muy alta (pintura Nextel, 3M ™) y una superficie con una emisividad muy baja (aluminio reflectante difuso). La figura 21 muestra el esquema general (1), una vista detallada de los diafragmas móviles y fijos, así como de la fuente recubierta con pintura Nextel (3M™) (2), una vista explosionada del dispositivo (3) y una fotografía del mismo. El dispositivo es portátil y debe conectarse a un ordenador que permita la demodulación de las señales mediante FFT.

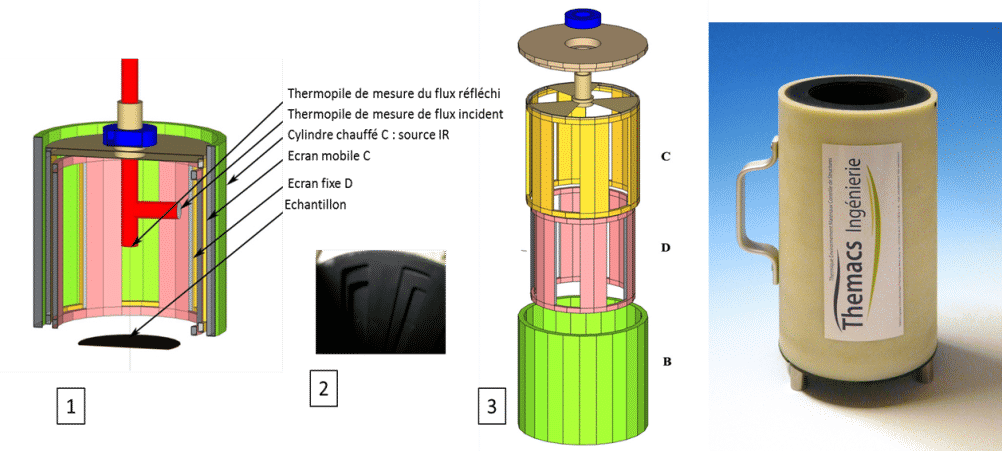
Figura 13

Medidor de emisiones EM3 de THEMACS Engineering

4 Información adicional

Existen varios documentos generales que complementan este estudio sobre mediciones de emisividad. Entre ellos se incluyen:
– «Measurement of Thermal Radiation Properties of Solids» (Medición de las propiedades de radiación térmica de los sólidos), [13]. Este documento recoge las contribuciones de un congreso celebrado en 1962 sobre las propiedades de radiación de los materiales. A pesar de la antigüedad de esta publicación, enumera de forma exhaustiva un gran número de medidores de emisividad utilizados en la aviación. Aunque las tecnologías han evolucionado mucho desde entonces, los principios de medición de estos dispositivos siguen siendo válidos.
– «Measurement Techniques for Thermal Radiation Properties» (Técnicas de medición de las propiedades de radiación térmica), [12]. De manera similar, este documento ofrece una visión general del estado de la técnica en 1990. Se describen nuevos dispositivos.

– «Spacecraft Thermal Control Coatings References» (Referencias sobre recubrimientos de control térmico para naves espaciales), [11]. Este documento de referencia de la NASA, uno de los más actuales, describe en primer lugar las magnitudes medidas. A continuación, se presenta un cálculo teórico que relaciona los índices complejos de los materiales y las propiedades de radiación. Después se describen los diferentes métodos de medición. Al final del documento se presentan mediciones realizadas en materiales que se utilizan con frecuencia en la industria aeroespacial. Al igual que el primer documento citado anteriormente, este documento también describe las propiedades ópticas en el rango visible, que también son importantes para deducir el balance térmico de un satélite expuesto a la radiación solar.

5 Bibliografía

Maldague, X.P. Teoría y práctica de la tecnología infrarroja para ensayos no destructivos. s.l.: Ed. Wiley, 2001.
Kauder, L. Referencias sobre recubrimientos de control térmico para vehículos espaciales, NASA-TP-2005-212792. 2005.
P. Lorrain, D.R. Corson. Champs et ondes électromagnétiques. s.l. : Armand Collin.
Rubin, M., Arasteh, D. y Hartmann, J. Una correlación entre la emisividad normal y hemisférica de recubrimientos de baja emisividad sobre vidrio. s.l. : Int. Comm. Heat Mass Transfer, 1987.
Blain, B. J. y Douglas, R. W. Constantes ópticas infrarrojas de los vidrios. 1965.
D. Janssen, J. Lohrengel. Investigación y desarrollo de un método para medir la emisividad del vidrio. s.l. : BCR Comunidad Europea, 1991. EUR 13487 EN.
GEOTTI-BIANCHINI, F. Emisividad hemisférica total del vidrio recubierto. s.l. : Comunidad Europea, 1993. EUR 14758 EN.
C. Fabron, A. Meurat. Medición de la emisividad hemisférica total a bajas temperaturas. s.l. : Simposio internacional sobre ensayos medioambientales para programas espaciales, Lieja, Bélgica, 2001.
J. Hameury, B. Hay, J. R. Filtz. Medición de la emisividad hemisférica total utilizando. s.l. : Int. J. Thermophys, 1607, 2007.
S. Moghaddam, J. Lawler, J. Currano. Método novedoso para medir la emisividad hemisférica total. s.l. : J. Thermophys. Heat Transfer, 2007.
A. Mazikowski, K .Chrzanowski. Método multibanda sin contacto para la medición de la emisividad. s.l. : Infrared Phys. Technol., 91, 2003.
L. Hanssen, S. Mekhontsev, V. Khromchenko. Dispositivo para la caracterización de la emisividad espectral infrarroja en el NIST, . s.l. : Thermosense XXVI, editado por Douglas D. Burleigh, K. Elliott Cramer, G. Raymond Peacock, Proc. of SPIE Vol. 5405, SPIE, Bellingham, WA, 2004.
L. Del Campo, R.B. Pérez-Saez, X. Esquisabel, I. Fernández, M.J. Tello. Nuevo dispositivo experimental para medir la emisividad espectral direccional en el rango infrarrojo en un entorno controlado. s.l. : Review Of Scientific Instruments, vol. 77, 113111, 1-8, 2006.
V. Vitkovskii, V. G. Gorshenev, Y. F. Potapov. Medición de la emisividad espectral direccional de materiales y recubrimientos en el rango infrarrojo del espectro. s.l. : Thermal Engineer , 245-248 Vol. 56-3, 2009.
A. Pantinakis, N. Kortsalioudakis. Un radiómetro infrarrojo sencillo y altamente sensible para medir la emisividad direccional total de materiales opacos a temperaturas cercanas a la temperatura ambiente. s.l. : International Journal of Thermophysics, 1843-1854 Vol. 22-6, 2001.
L.M. Hanssen, S. Kaplan. Medidores y estándares de reflexión difusa infrarroja en el NIST. s.l. : Anal. Chim. Acta, 289 , 1999.
D. Especel, S. Matteï. Medición de la emisividad total sin utilizar una referencia absoluta. s.l. : Infrared Phys. Technol., 777-784 volumen 37, 1996.
L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau. Medidor de emisividad infrarroja: principio y aplicaciones. s.l.: Meas. Sc. Tech., 2950, 2006.
M. Siroux. Desarrollo de técnicas para medir la emisividad de materiales opacos a temperatura ambiente. Enfoques radiométricos y calorimétricos en funcionamiento periódico. s.l.: Tesis doctoral, Universidad París 12, 1996.

Nuestro equipo le asesora para satisfacer mejor sus expectativas.

Contáctenos