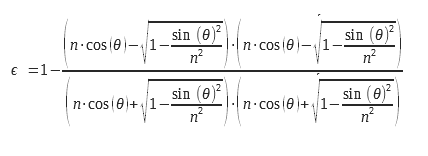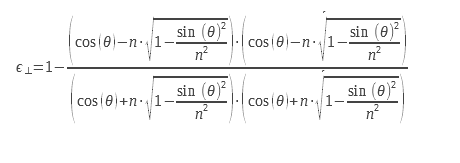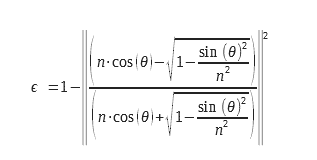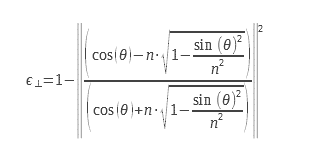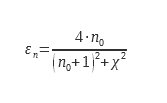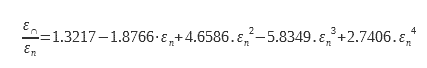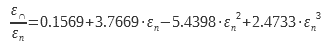Misuradell'emissività termicae
Misurazione dell’emissività termica
1. Definizioni delle diverse emissività
Le superfici dei materiali possono scambiare energia sotto forma di radiazione. La quantità di energia che una superficie può emettere dipende dalla sua temperatura e dalla sua natura. La legge di Planck specifica la luminanza energetica spettrale per una superficie teorica chiamata corpo nero :
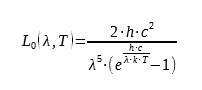
dove h = 6,62617.10−34 J.s è la costante di Planck, c è la velocità della luce nel mezzo considerato (si prenderà il valore di c nel vuoto: c = 299792458m.s−1) e k = 1,38066.10−23 J.K−1 è la costante di Boltzmann. La luminanza energetica spettrale L0 è espressa in W.m-3.sr-1.
Per un dato materiale, questa luminanza è ponderata da un coefficiente compreso tra 0 e 1 chiamato emissività. Si indica con ε.
Questo coefficiente può dipendere dalla lunghezza d’onda, dall’incidenza e dalla temperatura:
Le emissività sono classificate in base al dominio spaziale e spettrale della radiazione. Si definisce emissività totale l’emissività calcolata sull’intero spettro ed emissività monocromatica l’emissività calcolata per una sola lunghezza d’onda. Si definisce emissività emisferica l’emissività calcolata per tutte le direzioni ed emissività direzionale quella calcolata secondo una sola direzione.
1.1 Emissività monocromatica direzionale
L’emissività monocromatica direzionale indicata è il rapporto tra la luminanza del materiale e quella del corpo nero per una data direzione e lunghezza d’onda. È la grandezza che consente la descrizione più precisa di un dato materiale :
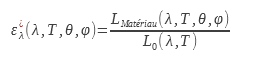
L0 non dipende dall’incidenza per un corpo nero.
La maggior parte dei materiali ha un’emissività che non dipende dall’orientamento e quindi non dipende da ϕ.
Per le superfici lisce questa emissività può dipendere dalla polarizzazione della luce.
1.2 Emissività monocromatica emisferica
L’emissività monocromatica emisferica è il rapporto tra la densità di potenza superficiale irradiata dalla superficie del materiale studiato e la densità di potenza superficiale irradiata dal corpo nero per una data lunghezza d’onda:
1.3 Emissività totale direzionale
L’emissività totale direzionale è il rapporto tra la luminanza irradiata dalla superficie del materiale studiato e la luminanza irradiata dal corpo nero sull’intero spettro elettromagnetico :
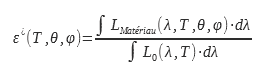
Questo valore di emissività è interessante per gli utenti di termocamere. Infatti, consente di collegare la luminanza in una direzione con la temperatura. Questo calcolo o questa misurazione dell’emissività può essere effettuato in una banda di lunghezza d’onda identica a quella della termocamera o in una data banda spettrale :
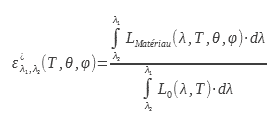
1.4 Emissività totale emisferica
L’emissività totale emisferica indicata con ε è il rapporto tra l’emissività totale emisferica del materiale e quella del corpo nero per tutte le lunghezze d’onda a una data temperatura :
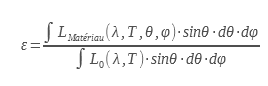
È proprio questa emissività che interessa i termotecnici per effettuare i bilanci termici delle pareti opache. Essa consente di calcolare gli scambi radiativi di una superficie portata alla temperatura T.
1.5 Casi particolari
Se l’emissività di un materiale non dipende dalla lunghezza d’onda, esso viene definito corpo grigio. Questa proprietà non si riscontra nella realtà e si definisce corpo grigio un corpo la cui emissività non varia nel campo spettrale studiato. Un corpo grigio le cui proprietà spettrali non variano in funzione della temperatura possiede un’emissività che non varia in funzione della temperatura. Al contrario, una superficie con un’emissività spettrale che varia con la lunghezza d’onda avrà un’emissività totale che varia con la temperatura, poiché lo spettro di radiazione del corpo nero varia con la temperatura.
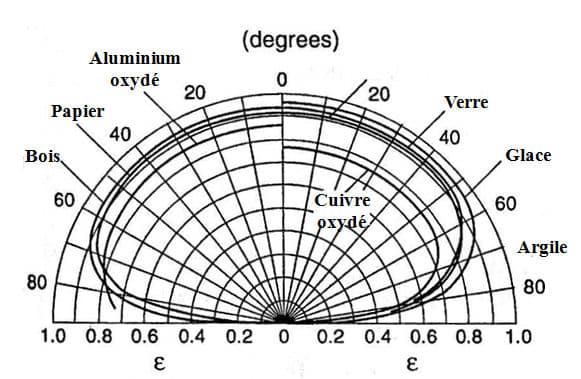
Come abbiamo appena visto, l’emissività di un materiale reale dipende generalmente anche dall’angolo di emissione. Non si tratta quindi di una superficie lambertiana. Per i dielettrici, tuttavia, l’emissività varia poco in un ampio intervallo angolare (da 0 a 60◦). In questo intervallo angolare, sono considerati lambertiani. Figura 1 secondo Maldague rappresenta l’emissività totale direzionale in funzione dell’angolo per un certo numero di materiali. Si può notare che essa non varia fino a un angolo di 60◦. Inoltre, la legge di variazione dell’emissività in funzione dell’angolo mostra una somiglianza di forma.
2. Calcolo dell’emissività a partire dall’indice complesso
La legge di conservazione dell’energia si traduce, nel caso della radiazione elettromagnetica, nella legge di Kirchhoff. In generale, questa legge collega, per una data lunghezza d’onda, il fattore di trasmissione, il fattore di riflessione direzionale emisferico all’assorbimento che in questo caso è uguale all’emissività :
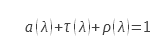
Dove a è il fattore di assorbimento spettrale, τ il fattore di trasmissione spettrale e ρ il fattore di riflessione direzionale emisferica.
Per un materiale opaco questa relazione diventa :
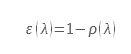
Poiché ε=a e per un materiale opaco τ=0.
L’equazione (8) è alla base di tutti i metodi indiretti di misurazione dell’emissività. Consente inoltre di calcolare l’emissività a partire dal fattore di riflessione stesso calcolato dalle relazioni di Fresnel. Questo approccio è valido solo per i diottri, ovvero per le superfici lisce.
2.1 Calcolo dell’emissività per le due polarizzazioni della luce
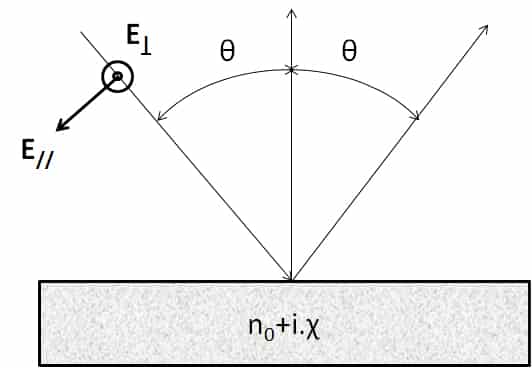
Per il diottro piano, è possibile calcolare l’emissività a partire dall’espressione dei coefficienti di riflessione, calcolati a partire dall’indice complesso, n = n0+i.χ. Questo calcolo dettagliato è riportato in Kauder sulla base delle equazioni di Maxwell. Queste espressioni sono dedotte dai coefficienti di Fresnel per la riflessione e sono riportate in Lorrain e Corson. Le equazioni 9 e 10 possono essere utilizzate con indici complessi, il che consente di utilizzarle per il calcolo dell’emissività dei metalli. Considerazioni relative alle condizioni al contorno a livello del diottro impongono di calcolare un coefficiente di riflessione e quindi di emissività per due polarizzazioni distinte. Queste polarizzazioni sono illustrate nello schema della Figura 2.
Per una luce non polarizzata, occorre calcolare la media aritmetica delle due emissività corrispondenti alle due polarizzazioni. Le espressioni delle due emissività per le due polarizzazioni sono riportate di seguito :
Si possono scrivere in un’altra forma :
2.2 Caso dei dielettrici
La Figura 3 tratta da Kauder mostra l’emissività direzionale in funzione dell’angolo per un dielettrico con indice di rifrazione pari a 1,5: ciò corrisponde a una permittività dielettrica relativa pari a 2,25:
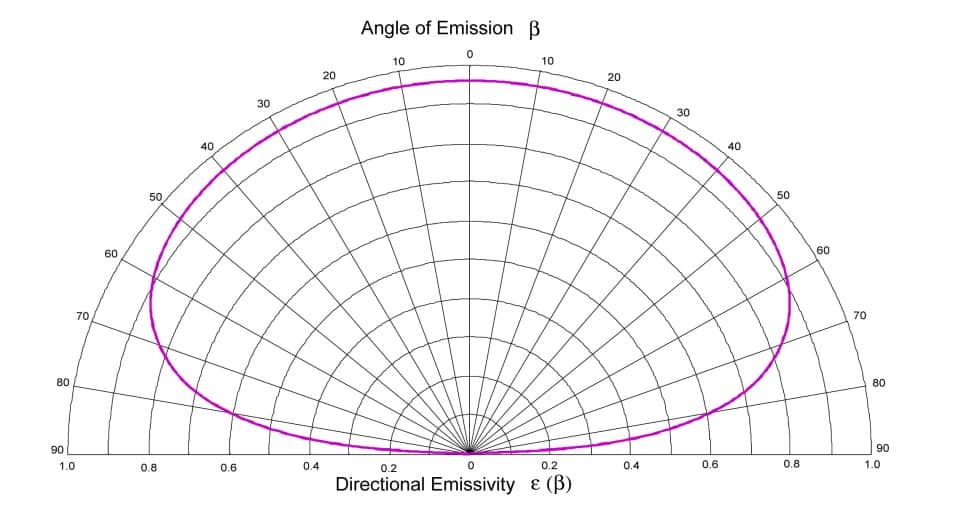
Figura 3
Emissività direzionale in funzione dell’angolo per un dielettrico con indice di rifrazione pari a 1,5 Kauder
Queste sono le caratteristiche tipiche di un vetro a base di borosilicati. Si osserva che la teoria fornisce lo stesso indicatore di emissività misurato sperimentalmente (Figura 1). Poiché l’unico parametro che può variare l’emissività di un diottro dielettrico liscio è l’indice di rifrazione reale, per un dato indice di rifrazione si avrà sempre lo stesso indicatore di emissività. Di conseguenza, è possibile calcolare l’emissività emisferica mediante integrazione sull’intero emisfero.
Il rapporto tra l’emissività emisferica e l’emissività direzionale normale dipende quindi solo dall’indice di rifrazione, e quindi solo dall’emissività direzionale normale (Figura 1). È quindi possibile dedurre l’emissività emisferica dall’emissività direzionale normale e viceversa. Questi rapporti sono riportati nella norma NF EN 12898 relativa alla determinazione dell’emissività per il vetro da costruzione. Questo studio può essere utilizzato per un dielettrico non liscio con una buona approssimazione. Infatti, la rugosità influisce solo in misura minima sull’indicatore di emissività di un dielettrico. Queste considerazioni saranno riprese nella parte 1.9.
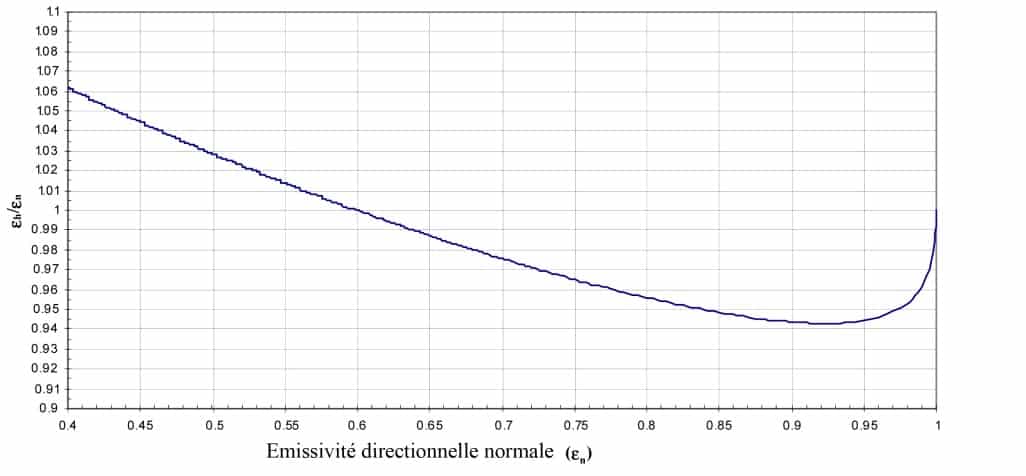
Figura 4
Rapporto tra l’emissività emisferica e l’emissività direzionale normale in funzione dell’emissività direzionale normale per i dielettrici lisci Kauder
2.3 Caso dei metalli e dei conduttori
Allo stesso modo, è possibile tracciare l’indicatore di emissività per un diottro aria/metallo. Si ottiene un indicatore di emissività teorico simile a quello che si può ottenere su un metallo come l’alluminio. Quella rappresentata nella Figura 5 tratta da Kauder è calcolata per un indice di rifrazione tipico di un metallo come l’alluminio. : n = 5.7 + 9.7i. La corrispondenza tra l’emissività emisferica e l’emissività direzionale normale esiste anche per i conduttori, tuttavia l’indicatore di emissività è diverso. È quindi necessario trattare i conduttori separatamente dai dielettrici per determinare il rapporto tra le due emissività. Questo studio non può essere utilizzato per un conduttore non liscio. Infatti, la rugosità influisce notevolmente sull’indicatore di emissività di un metallo, poiché l’emissività di un metallo varia notevolmente in base alla sua rugosità. Si rimanda al riferimento [30] per uno studio più dettagliato sull’emissività dei metalli in funzione della rugosità.
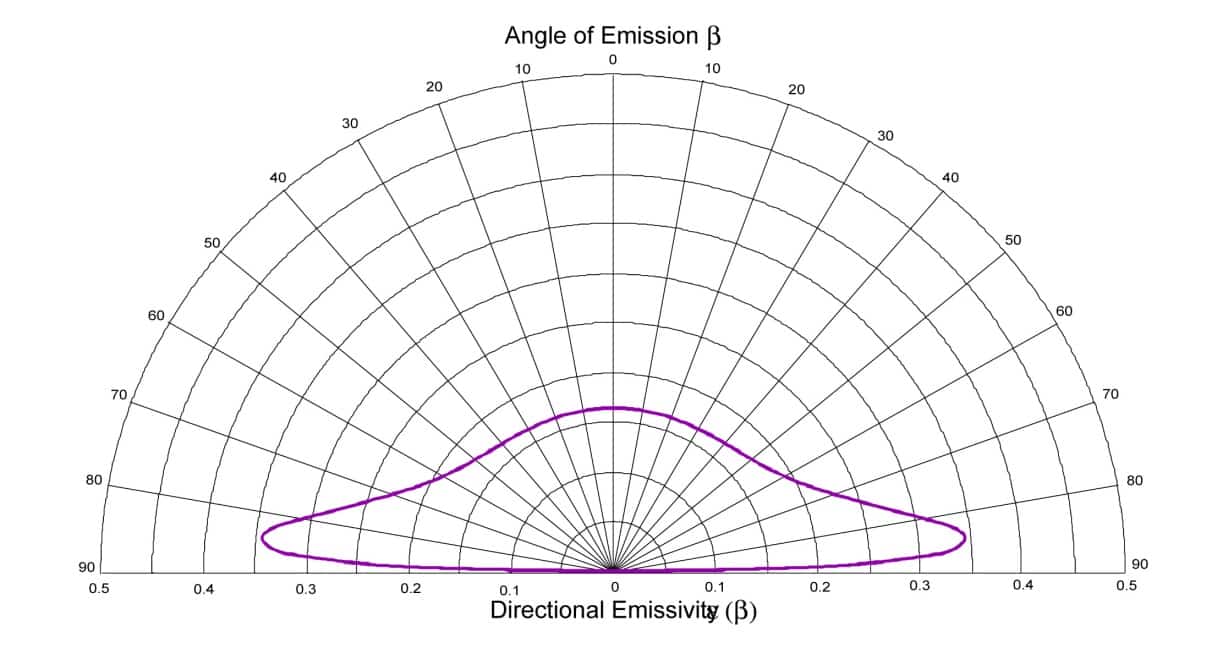
Figura 5
Emissività direzionale in funzione dell’angolo per un metallo con indice di rifrazione: n = 5,7+9,7. i
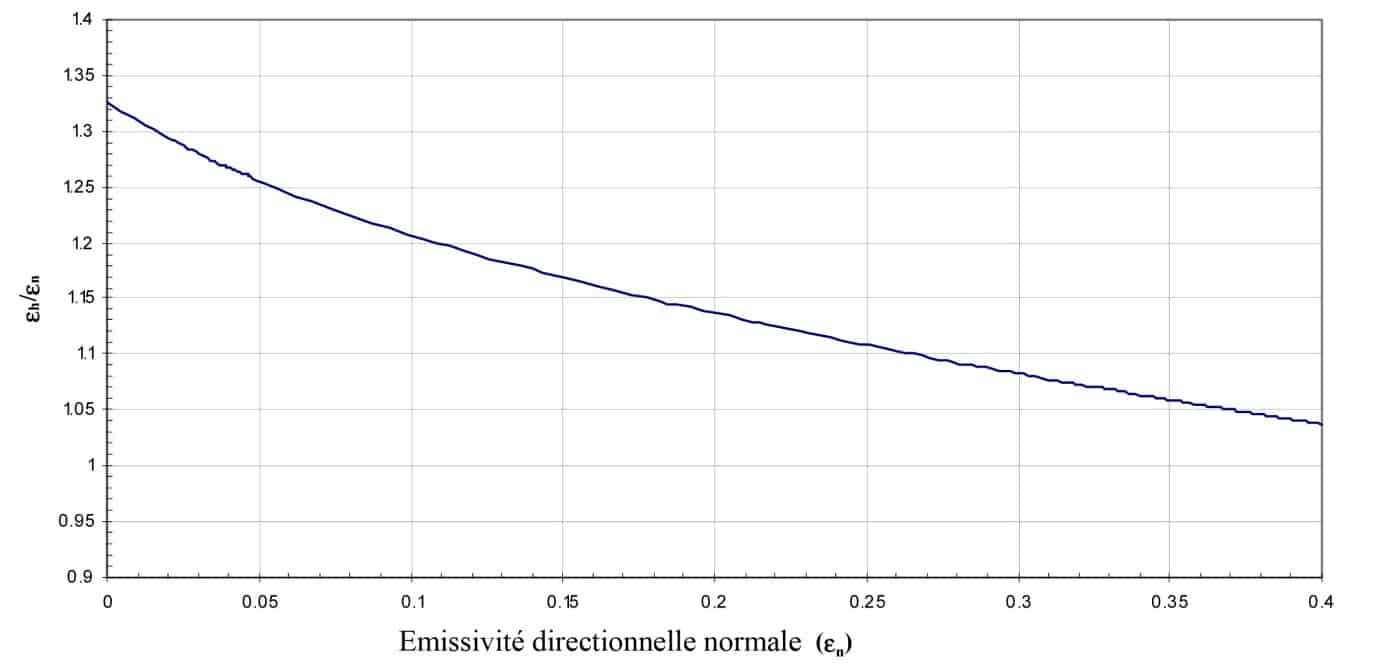
Figura 6
Rapporto tra l’emissività emisferica e l’emissività direzionale normale in funzione dell’emissività direzionale normale per i conduttori lisci (2)
Per i conduttori, due parametri, n0 e χ, possono variare. La Figura 6 mostra una curva teorica ottenuta variando la parte immaginaria dell’indice. Per i casi più complessi e soprattutto per le superfici ruvide, studi sperimentali hanno permesso di tabulare i valori.
2.4 Relazione tra emissività direzionale normale ed emissività emisferica
Per motivi di praticità, spesso si misura l’emissività direzionale con incidenza quasi normale. Tuttavia, è spesso necessario ottenere l’emissività emisferica. Quest’ultima è l’integrazione su tutti gli angoli solidi utili dell’emissività direzionale.
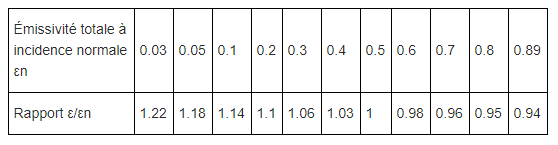
Se non è possibile misurarla su tutte le incidenze, si deve poter dedurre l’emissività emisferica dall’emissività direzionale in incidenza quasi normale. Questo calcolo è teoricamente possibile per i diottri lisci dei dielettrici, poiché l’emissività dipende solo dall’indice normale (Figura 1). I valori della Tabella 1 sono tratti dalla norma ISO 12898. Essa è destinata alla misurazione dell’emissività dei vetri.
Tabella 1 Fattori che consentono di calcolare l’emissività totale emisferica a partire da εn per una superficie dielettrica liscia
Alcuni studi importanti hanno permesso di documentare questo coefficiente ε∩/εn. Per le superfici lisce a bassa emissività (tipicamente i metalli). Rubin e Hartmann hanno utilizzato strati di argento e In2O3 su vetro. È stata ottenuta un’espressione analitica utilizzando i dati sperimentali e le relazioni di Kramer Kroning :
Per i dielettrici con emissività εn compresa tra 0,68 e 0,98 viene utilizzata un’altra espressione :
Questi dati sono stati raccolti e integrati in due rapporti di recercia europei. Hanno permesso di fornire i dati necessari alla redazione della norma ISO 12898.
Questi dati sono riportati nel grafico. La curva contrassegnata con la dicitura Metalli corrisponde all’equazione (14), quella contrassegnata con la dicitura Dielettrico all’equazione (15). Anche i valori riportati nella norma ISO 13898 sono riportati in questo grafico.
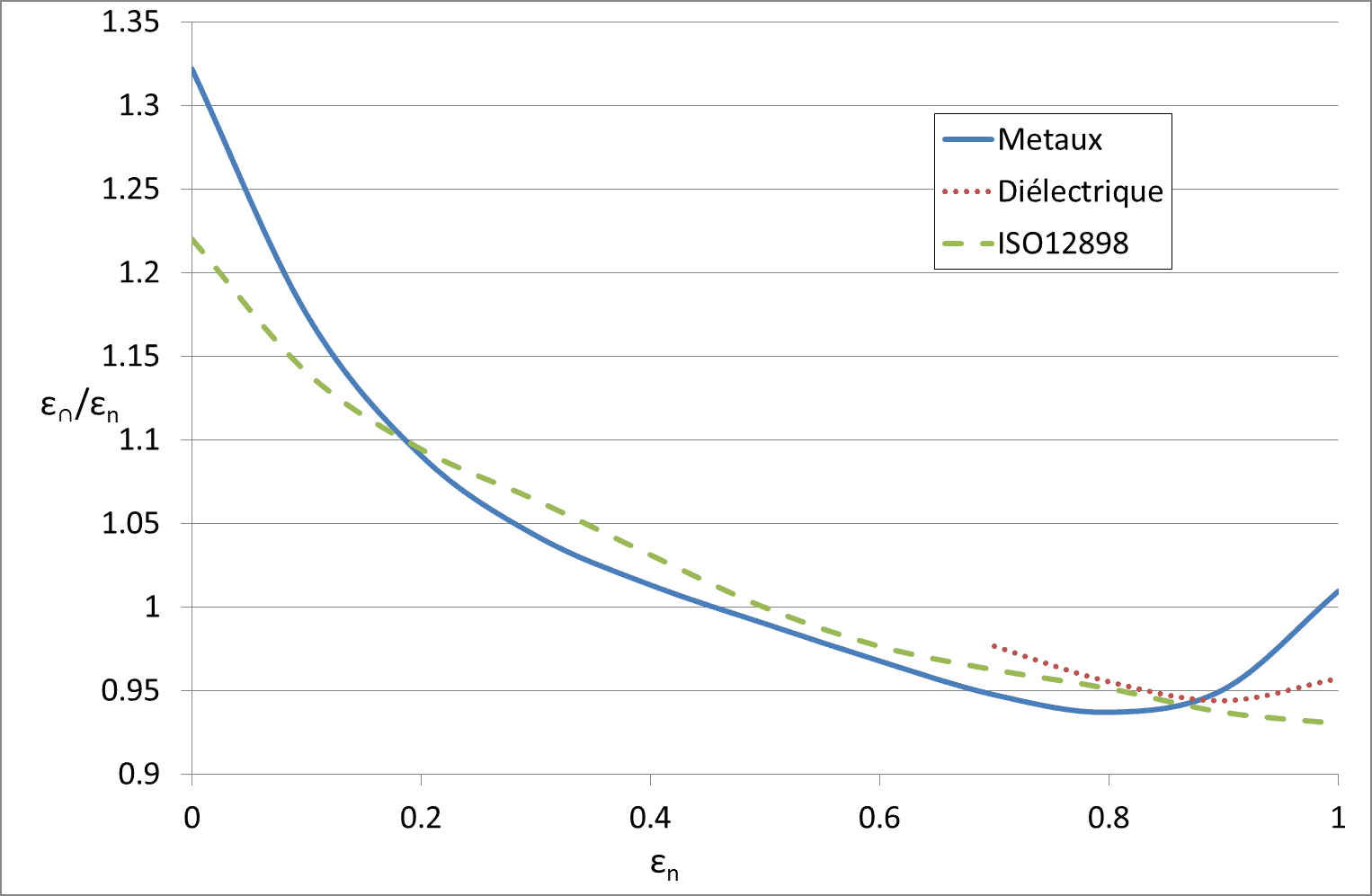
Figura 7
Rapporto tra ε ed εn secondo le diverse fonti
3. I diversi metodi di misurazione dell’emissività termica
3.1 Classificazione dei metodi
In questo capitolo trattiamo i metodi di misurazione dell’emissività. Essi sono stati classificati in base al principio fisico della misurazione. Abbiamo separato i metodi cosiddetti diretti dai metodi cosiddetti indiretti. I metodi diretti sono quelli in cui si misura direttamente la potenza irradiata dalla superficie: si tratta dei metodi calorimetrici e radiometrici.
I metodi indiretti sono quelli in cui le proprietà delle superfici nel campo spettrale dell’infrarosso sono dedotte dalle proprietà ottiche mediante riflettometria: è il caso di tutti gli altri metodi. Tutti gli apparecchi commerciali utilizzano questi metodi indiretti in un modo o nell’altro. I metodi diretti sono limitati solo dal dispositivo sperimentale utilizzato. I metodi indiretti soffrono di distorsioni intrinseche al metodo di misurazione stesso.
3.2 Metodo calorimetrico
Il metodo calorimetrico consente di valutare i trasferimenti radiativi senza trascurare alcun impatto o lunghezza d’onda. Consiste nell’effettuare un bilancio energetico delle perdite radiative del campione studiato quando queste sono le uniche in gioco. Si tratta di un metodo diretto e assoluto, ovvero non richiede un riferimento di emissività standard per
ottenere l’emissività del campione. Questo metodo rimane comunque complesso. Infatti, per eliminare i trasferimenti per conduzione e convezione, è necessario collocare il campione in atmosfera ridotta (tipicamente 10−5 mbar). Il campione viene riscaldato e mantenuto alla temperatura alla quale si desidera conoscere l’emissività. Per mantenere la temperatura, è necessario fornirgli
una potenza:
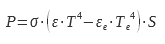
dove P è la potenza dissipata dal campione, ε è la sua emissività, σ è la costante di Stefan-Boltzmann, T è la temperatura del campione, εe è l’emissività della camera, Te è la temperatura della camera e S è la superficie emissiva del campione.
La potenza necessaria per mantenere il campione alla temperatura alla quale si desidera conoscere l’emissività è fornita elettricamente sotto forma di effetto Joule. La Figura 1 Figura 8 rappresenta schematicamente un dispositivo di misurazione dell’emissività con il metodo calorimetrico. La camera (F) è mantenuta sotto vuoto mediante un dispositivo di pompaggio collegato alla camera tramite il tubo A.
I cavi elettrici di alimentazione e misurazione (B) sono collegati al campione tramite una morsettiera C. Quest’ultima funge da protezione per evitare perdite per conduzione. La temperatura di questa morsettiera è mantenuta e regolata alla stessa temperatura del campione. In questo modo, la potenza dissipata per conduzione dai cavi elettrici di alimentazione e misurazione tra la morsettiera e il campione è pari a zero a causa dell’assenza di gradiente di temperatura.
Il disco campione con superficie radiante nota è sospeso nella camera. L’involucro E è un criostato coibentato, solitamente riempito con azoto liquido. L’elio viene utilizzato quando si desidera misurare l’emissività a basse temperature (inferiori a 250 K) per l’industria spaziale. Un dispositivo di questo tipo è descritto in Fabron e Meurat. L’involucro F è rivestito internamente con un rivestimento ad alta emissività e emissività spettrale che varia poco con la lunghezza d’onda. La scelta della temperatura del criostato è guidata dalla necessità di avere ε.T4 ≫ εe.Te4. La temperatura ideale deve consentire di ottenere una polarizzazione ben inferiore all’incertezza di misura del dispositivo. Dalla relazione 16 è possibile dedurre l’emissività :
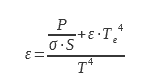
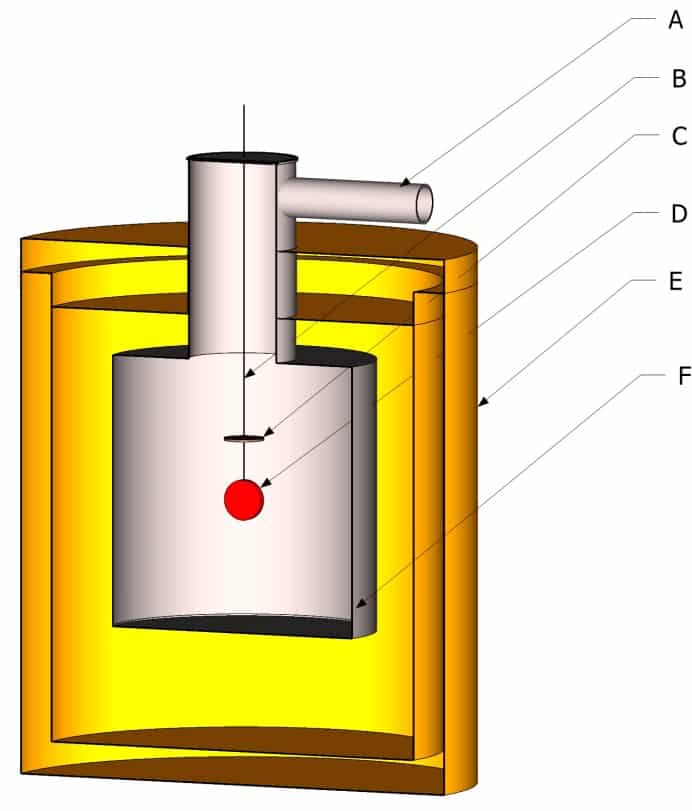
Figura 8
Schema di principio del metodo calorimetrico
Il metodo calorimetrico è l’unico che consente una determinazione diretta dell’emissività totale emisferica. Viene presa in considerazione l’intera radiazione. Il fatto che non richieda alcun riferimento o standard di emissività lo rende un metodo di riferimento.
Questo metodo rimane tuttavia complesso e lungo da implementare. Sarebbe difficile costituire una banca dati sull’emissività utilizzando solo questo metodo. La principale fonte di incertezza è la misurazione della temperatura superficiale. Questa può essere estrapolata misurando il gradiente di temperatura all’interno del campione utilizzando diversi sensori .
Inoltre, è necessario disporre di campioni calibrati in base alle dimensioni per poterli inserire nel dispositivo di misurazione. Altri dispositivi più semplici sono descritti in Moghaddam, Lawler e Currano.
3.3 Metodo radiometrico
3.3.1 Metodo di misurazione diretta del flusso/della luminanza
Questo metodo consiste nel confrontare la luminanza di un campione con quella di un corpo nero portato alla stessa temperatura. Il dispositivo è descritto nella Figura 9Figura 1. In questa figura, il campione A viene portato alla temperatura alla quale si desidera misurare l’emissività. Questo viene posto in una camera refrigerata B con le stesse condizioni di temperatura del metodo calorimetrico (ε.T4 ≫ εe.Te4). Un corpo nero E portato alla stessa temperatura del campione costituisce il riferimento di luminanza.
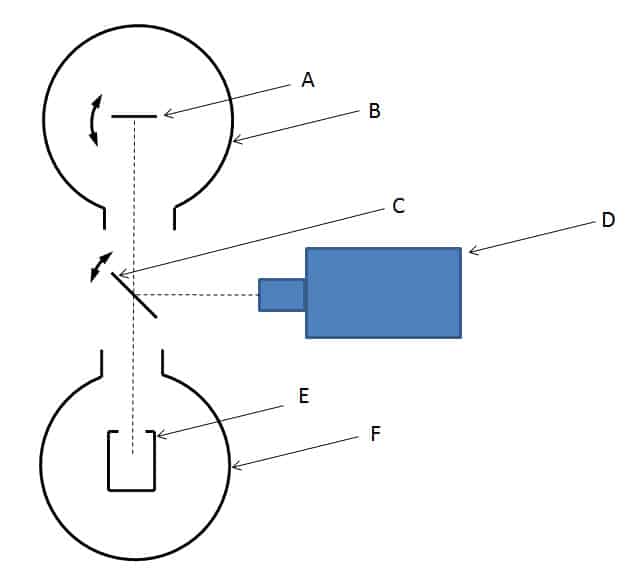
Figura 9
Metodo radiometrico
Si misura successivamente la luminanza del corpo nero e quella del campione grazie allo specchio ribaltabile C. Il rapporto tra queste due luminanze fornisce l’emissività. Il corpo nero è collocato in una camera isolata termicamente senza condizioni di temperatura. È possibile effettuare la misurazione con un corpo nero avente una temperatura diversa da quella del campione. In questo caso si applica un rapporto tra le temperature alla quarta potenza.
Le due luminanze vengono misurate con il rilevatore D. Questo può essere un rilevatore a infrarossi a banda larga (come una termopila) per misurare l’emissività totale. Questo rilevatore può essere dotato di una ruota portafiltro per misura l’emissività spettrale per diverse lunghezze d’onda.
L’insieme dei dispositivi di misurazione dell’emissività mediante confronto con un corpo nero del NIST (National Institute of Standards and Technology, Gaithersburg, Maryland, Stati Uniti) è presentato in Novel method for measurement of total hemispherical emissivity. In questo dispositivo non è presente uno specchio ribaltabile, il sistema di rilevamento viene spostato di fronte alle superfici da misurare e ai corpi neri di riferimento tramite un carrello. Questo dispositivo è un punto di riferimento nel settore per le misurazioni dell’emissività a temperature comprese tra 600 K e 1400 K.
L’emissometro descritto da Campo, Esquisabel, Fernandez e Tello utilizza uno spettrometro a infrarossi con trasformata di Fourier. La luminanza viene quindi misurata in una sola direzione, consentendo di misurare l’emissività direzionale. Per misurare diversi angoli di incidenza e risalire all’emissività emisferica, alcuni dispositivi consentono di ruotare il campione: è il caso del dispositivo descritto in New experimental device for infrared spectral directional emissivity measurements in a controlled environment. Lo spettrometro può anche essere sostituito da un monocromatore come il dispositivo descritto in Measurement of Spectral Directional Emissivity of Materials and Coatings in the Infrared Region of Spectrum.
La misurazione radiometrica a temperatura ambiente richiede che il campione sia posto in un criostato a bassissima temperatura e sotto vuoto per evitare la condensa. Un dispositivo originale che evita questo problema è descritto in A Simple High-Sensitivity Radiometer in the Infrared for Measurements of the Directional Total Emissivity of Opaque Materials at Near-Ambient Temperatures.
Il principio rimane lo stesso, tuttavia le misurazioni vengono effettuate a temperatura ambiente e il flusso misurato viene poi corretto sulla base delle misurazioni della temperatura della camera e del chopper. Ciò semplifica notevolmente il dispositivo, ma introduce ulteriori fonti di incertezza.
3.3.2 Metodo radiometrico periodico
Il metodo radiometrico periodico consiste nel modulare leggermente la temperatura del campione intorno alla temperatura alla quale si desidera conoscere l’emissività. In questo modo è possibile separare il flusso riflesso dal flusso proprio del campione. Questo è il principio del metodo radiometrico modulato.
Per ottenere l’emissività, è necessario confrontare il flusso misurato con quello di una superficie di emissività nota. Un altro metodo consiste nel modulare anche una sorgente emisferica a una frequenza diversa dalla frequenza di modulazione del campione. Effettuando la misurazione su due campioni sconosciuti, è possibile ottenere il valore dell’emissività e della riflettività. Questo metodo non richiede un riferimento di emissività per effettuare la misurazione. Il metodo radiometrico periodico è descritto in dettaglio in [20].
3.4 Metodi riflettometrici
Il metodo riflettometrico consiste nel misurare il coefficiente di riflessione emisferica direzionale o il coefficiente di riflessione direzionale emisferico al fine di calcolare l’emissività direzionale per una direzione equivalente a quella utilizzata per misurare il coefficiente di riflessione. Questo calcolo si basa sulla legge di Kirchhoff (2). Tale legge può essere enunciata come segue: per una superficie opaca in equilibrio termico con l’ambiente circostante, è possibile scrivere per una lunghezza d’onda λ :
![]()
L’equilibrio termico impone una temperatura identica per l’ambiente e per la superficie in questione. È possibile estendere
questa relazione a un intervallo di lunghezze d’onda.
È possibile calcolare questo coefficiente di riflessione misurando la riflettanza per tutte le lunghezze d’onda ed effettuando l’integrazione ponderata dall’emissività del corpo nero, oppure assicurandosi di misurare la riflettanza con una sorgente luminosa che abbia la stessa distribuzione spettrale energetica del corpo nero alla temperatura considerata. È inoltre necessario assicurarsi che il rilevatore a infrarossi utilizzato abbia una risposta sufficientemente costante nel campo spettrale considerato.
A condizione che la riflettanza spettrale non vari con la temperatura, è possibile calcolare tale riflettanza senza preoccuparsi della temperatura del campione. Vedremo diversi metodi di misurazione dell’emissività basati sulla misurazione della riflettanza.
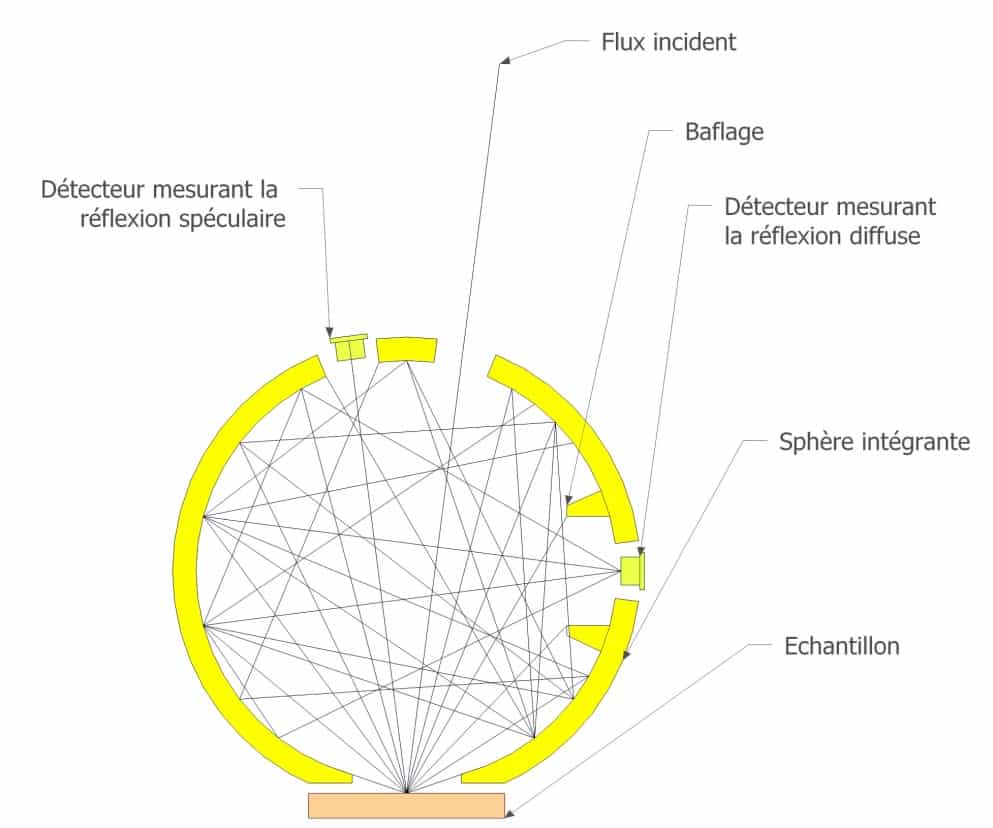
Figura 10
Schema di un dispositivo di misurazione della riflessione direzionale emisferica mediante il metodo della sfera integrale
3.4.1 Metodi a specchio?
3.4.2 Metodo della sfera integrale
La Figura 10 mostra il funzionamento di una sfera integrale. Questa deve essere rivestita internamente con un rivestimento riflettente e diffusivo. Il campione viene illuminato con una sorgente a infrarossi in una direzione data vicina alla normale. L’angolo di incidenza nelle sfere integratrici commerciali è compreso tra 8 e 12 gradi. Una volta che la luce ha raggiunto il campione, viene diffusa in tutte le direzioni in base all’indicatore di riflettanza del materiale. Dopo molteplici riflessioni, la luce raggiunge il rilevatore posto sul lato. In teoria, il rilevatore misura quindi la quasi totalità del flusso riflesso dal campione. Un sistema di deflessione impedisce al rilevatore di vedere direttamente il campione, in modo da non interferire con la misurazione. È possibile posizionare un rilevatore simmetricamente rispetto alla sorgente per misurare la riflessione speculare.
Questo è facoltativo e, su alcune sfere, è possibile inserire nella posizione della riflessione speculare una porzione di superficie diffondente della stessa natura della sfera oppure lasciarla aperta. Nel primo caso, si misura l’intero flusso riflesso (diffuso e speculare), mentre nel secondo caso si misura solo il flusso diffuso.
Per sottrazione è possibile ottenere il coefficiente di riflessione speculare. Per effettuare una misurazione del coefficiente di riflessione è necessario calibrare il dispositivo con un riferimento di riflettanza. Si utilizza lo stesso tipo di rivestimento utilizzato per la sfera. Si tratta generalmente di una superficie metallica sabbiata o microgranulata ricoperta da uno strato d’oro. Un dispositivo di questo tipo è utilizzato dal NIST. È descritto in Infrared diffuse reflectance instrumentation and standards at NIST.
3.4.3 Metodo che utilizza una sorgente modulata
In precedenza, per il metodo radiometrico, quando si desiderava misurare il flusso emesso dalla superficie era necessario liberarsi dal flusso proveniente dall’ambiente radiativo attorno al campione. Quest’ultimo veniva quindi posto in una camera raffreddata a una temperatura Te, in modo da garantire σ.T4>>σ.Te4. Questa condizione vincolante è tuttavia facile da ottenere grazie a una camera raffreddata ad acqua per temperature del campione dell’ordine di 1000 K. Tuttavia, quando si desidera misurare l’emissività a temperatura ambiente, è necessario raffreddare la camera a temperature criogeniche. Per evitare questa ulteriore complessità, è possibile modulare la temperatura del campione da misurare intorno alla temperatura alla quale si desidera conoscere l’emissività. In questo caso si rileva il flusso modulato emesso e lo si confronta con un’ampiezza di modulazione uguale a quella emessa da una superficie di riferimento. Quando non è possibile modulare la temperatura del campione, è possibile utilizzare un metodo riflettometrico e modulare il flusso utilizzato per misurare il fattore di riflessione. Questi metodi sono descritti in Infrared emissivity measurement device : Principle and applications, e un esempio specifico di realizzazione in Sviluppo di tecniche di misurazione dell’emissività dei materiali opachi a temperatura ambiente.
Per separare il flusso proprio del campione dal flusso riflesso, su quest’ultimo viene inviato un flusso emisferico modulato in frequenza. Il principio consiste nel produrre un flusso infrarosso emisferico modulato attorno al campione studiato e misurare, in una direzione, il flusso riflesso dalla superficie del materiale utilizzando una termopila. Lo schema della Figura 11 mostra il principio del dispositivo. Il dispositivo viene preventivamente calibrato utilizzando un materiale di riferimento noto. La Figura 12 mostra lo schema dell’apparecchio sviluppato dal CERTES e una foto dello strumento. La cavità è costituita da un cubo cavo in alluminio aperto nella parte inferiore. La temperatura delle pareti è modulata grazie a elementi ad effetto Peltier. La misurazione del flusso riflesso avviene attraverso un’apertura praticata nella parte superiore del dispositivo mediante una termopila dotata di una lente in KRS5.
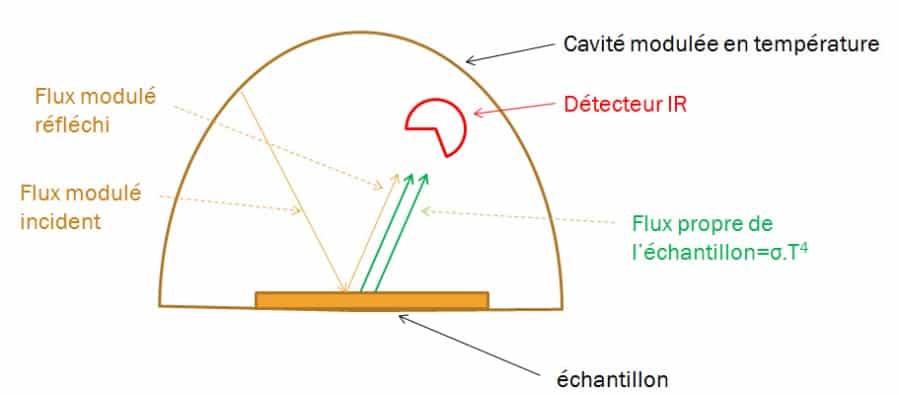
Figura 11
Principio del metodo di misurazione riflettometrico con una sorgente modulata
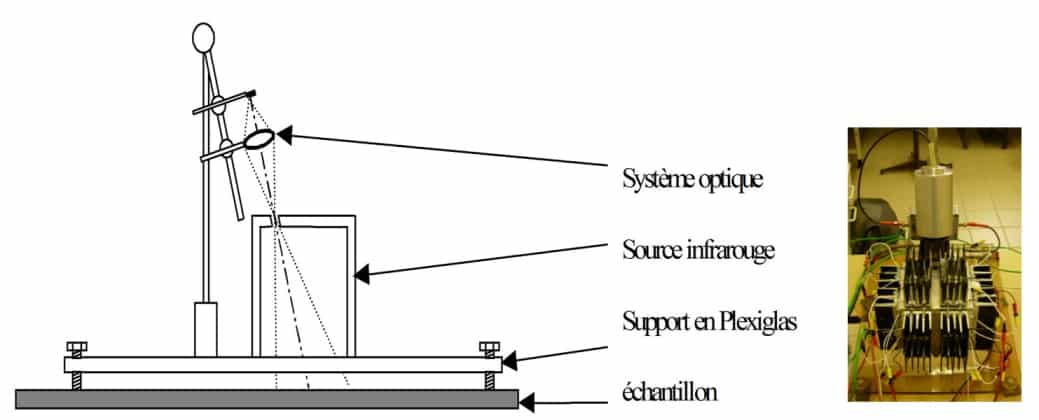
Figura 12
Schema e foto del dispositivo di misurazione sviluppato dal CERTES
Un altro metodo per modulare il flusso emisferico consiste nell’utilizzare un chopper tridimensionale. Questo dispositivo è stato brevettato dall’Università ParisXII. Il dispositivo è illustrato di seguito.
EM3 di THEMACS Ingegneria :
Il principio di funzionamento di questo apparecchio è quello descritto in precedenza. Consiste nel modulare una sorgente di radiazione emisferica tramite alette mobili. Ciò evita di modulare la cavità in temperatura, operazione molto lenta. Lo schema in figura illustra il principio di modulazione. La sorgente è il cilindro B riscaldato a una temperatura leggermente superiore alla temperatura ambiente.
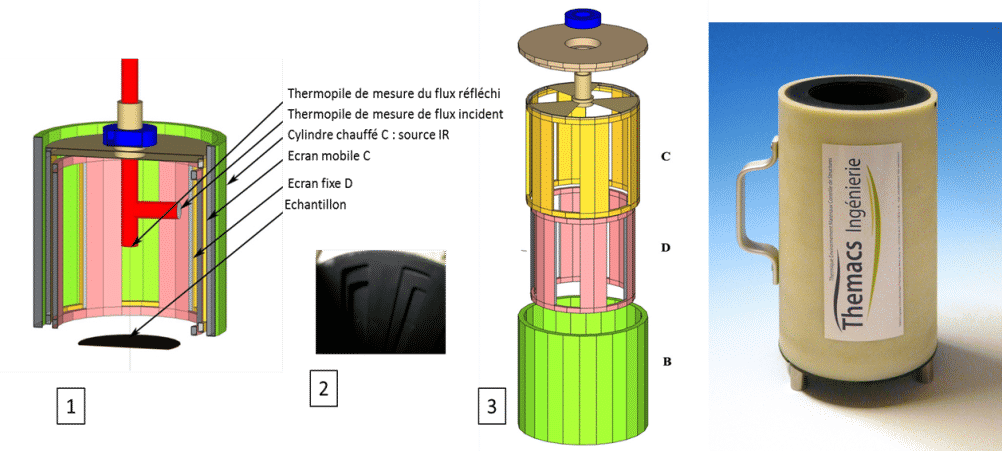
Figura 13
Emissometro EM3 di THEMACS Ingénierie
Il cilindro mobile C e lo schermo fisso D oscurano la sorgente emisferica a una frequenza di 10 Hz per la parete cilindrica (presenza di 6 finestre) e di 5 Hz per la parte superiore (presenza di 3 finestre). In questo modo è possibile distinguere un materiale speculare da un materiale diffusivo. Una termopila misura il flusso incidente e un’altra il flusso riflesso. Il rapporto del flusso riflesso non dipende dal livello emesso dalla sorgente.
Questo emissometro deve essere preventivamente calibrato utilizzando due superfici con emissività nota. Generalmente si utilizza una superficie ad alta emissività (vernice Nextel, 3M™) e una superficie a bassissima emissività (alluminio diffusivo). La figura mostra lo schema generale (1), un dettaglio delle alette mobili e fisse e della sorgente ricoperte di vernice Nextel (3M™) (2), una vista esplosa del dispositivo (3) e una foto dell’apparecchio. Il dispositivo è portatile e deve essere collegato a un computer che consenta di demodulare i segnali tramite FFT.