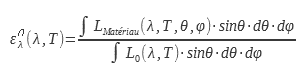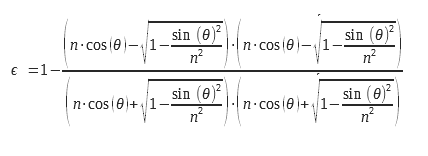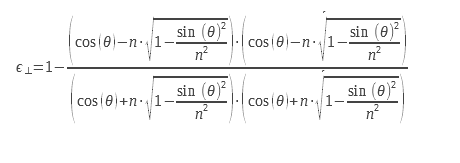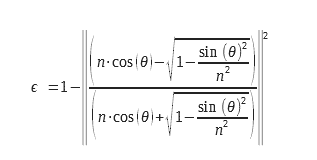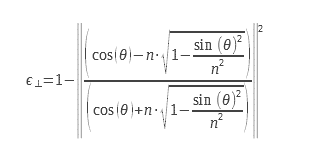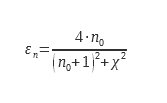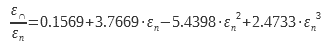Messung des Wärmeemissionsgrads

Messung der thermischen Emissivität

1. 1 Unterschiedliche Emissionsgrade

Die Oberflächen von Materialien können Energie in Form von Strahlung austauschen. Die Energiemenge, die eine Oberfläche abgeben kann, hängt von ihrer Temperatur und ihrer Beschaffenheit ab. Das Plancksche Strahlungsgesetz gibt die spektrale Energieluminanz für eine theoretische Oberfläche an, die als schwarzer Körper bezeichnet wird :

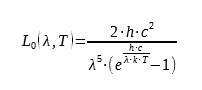
wobei h = 6,62617·10−34 Js die Plancksche Konstante, c die Lichtgeschwindigkeit im betrachteten Medium (wir nehmen den Wert von c im Vakuum: c = 299792458 m·s−1) und k = 1,38066·10−23 JK−1 die Boltzmannsche Konstante ist. Die spektrale Energieluminanz L0 wird in Wm-3.sr-1 ausgedrückt.

Für ein bestimmtes Material wird diese Luminanz mit einem Koeffizienten zwischen 0 und 1 gewichtet und als Emissivität bezeichnet. Wir schreiben sie mit ε.

Dieser Koeffizient kann von der Wellenlänge, dem Einfallswinkel und der Temperatur abhängen: ε(λ,T,θ,φ).
Emissionsgrade werden nach den räumlichen und spektralen Bereichen der Strahlung klassifiziert. Wir bezeichnen den über das gesamte Spektrum berechneten Emissionsgrad als Gesamtemissionsgrad und den für eine einzelne Wellenlänge berechneten Emissionsgrad als monochromatischen Emissionsgrad. Wir bezeichnen den für alle Richtungen berechneten Emissionsgrad als hemisphärischen Emissionsgrad und den in einer Richtung berechneten Emissionsgrad als gerichteten Emissionsgrad.

1.1 Richtungsabhängige monochromatische Emissivität

Die richtungsabhängige monochromatische Emissivität ε_λ^| ist das Verhältnis zwischen der Leuchtdichte des Materials und der eines schwarzen Körpers für eine bestimmte Richtung und Wellenlänge. Sie ist die Größe, die die genaueste Beschreibung für ein bestimmtes Material ermöglicht:

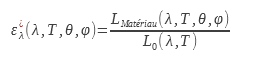
L0 ist für einen schwarzen Körper unabhängig von der Einfallsrichtung.
Die meisten Materialien haben eine Emissivität, die nicht von der Ausrichtung und daher auch nicht von ϕ abhängt.
Bei glatten Oberflächen kann diese Emissivität von der Polarisation des Lichts abhängen.

1.2 Hemisphärische monochromatische Emissivität

Die hemisphärische monochromatische Emissivität ist das Verhältnis zwischen der von der Oberfläche des untersuchten Materials abgestrahlten Oberflächenleistungsdichte und der von einem schwarzen Körper für eine bestimmte Wellenlänge abgestrahlten Oberflächenleistungsdichte:

1.3 Gesamtemissionsgrad

Die Gesamtemissionsfähigkeit ist das Verhältnis zwischen der von der Oberfläche des untersuchten Materials abgestrahlten Leuchtdichte und der von einem schwarzen Körper über das gesamte elektromagnetische Spektrum abgestrahlten Leuchtdichte :

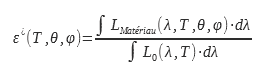
Dieser Wert der Emissivität ist für Nutzer von Wärmebildkameras von Interesse. Er ermöglicht es nämlich, die Leuchtdichte in einer Richtung mit der Temperatur in Verbindung zu bringen. Diese Berechnung oder Messung der Emissivität kann in einem Wellenlängenbereich erfolgen, der mit dem der Kamera identisch ist, oder in einem bestimmten Spektralbereich :

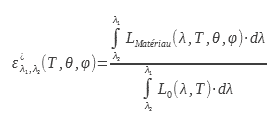
1.4 Gesamtemissionsgrad

Der Gesamtemissionsgrad ε ist das Verhältnis zwischen der Gesamtemittanz des Materials und der eines schwarzen Körpers für alle Wellenlängen bei einer bestimmten Temperatur :

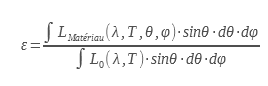
Dieser Emissionsgrad ist für Thermiker interessant, um die Wärmebilanz undurchsichtiger Wände zu berechnen. Er ermöglicht die Berechnung des Strahlungsaustauschs einer Oberfläche, die auf die Temperatur T gebracht wurde.

1.5 Sonderfälle

Wenn die Emissivität eines Materials nicht von der Wellenlänge abhängt, bezeichnet man dieses als Graukörper. Diese Eigenschaft kommt in der Realität nicht vor, daher bezeichnen wir als Graukörper einen Körper, dessen Emissivität im untersuchten Spektralbereich nicht variiert. Ein Graukörper, dessen spektrale Eigenschaften nicht in Abhängigkeit von der Temperatur variieren, hat eine Emissivität, die ebenfalls nicht in Abhängigkeit von der Temperatur variiert. Umgekehrt hat eine Oberfläche mit einer sich mit der Wellenlänge ändernden spektralen Emissivität eine sich mit der Temperatur ändernde Gesamtemissivität, da sich das Strahlungsspektrum eines schwarzen Körpers mit der Temperatur ändert.

Wie wir gerade gesehen haben, hängt die Emissivität eines realen Materials im Allgemeinen auch vom Emissionswinkel ab. Es handelt sich also nicht um eine Lambert’sche Oberfläche. Bei Dielektrika ändert sich die Emissivität jedoch nur geringfügig über einen großen Winkelbereich (von 0 bis 60◦). In diesem Winkelbereich werden sie als Lambertsche Oberflächen betrachtet. Abbildung 1 aus (1) zeigt die gesamte Richtungsemissionsfähigkeit als Funktion des Winkels für eine Reihe von Materialien. Wir können sehen, dass sie bis zu einem Winkel von 60◦ nicht variiert. Darüber hinaus zeigt das Gesetz der Variation der Emissionsfähigkeit als Funktion des Winkels eine Ähnlichkeit in der Form.

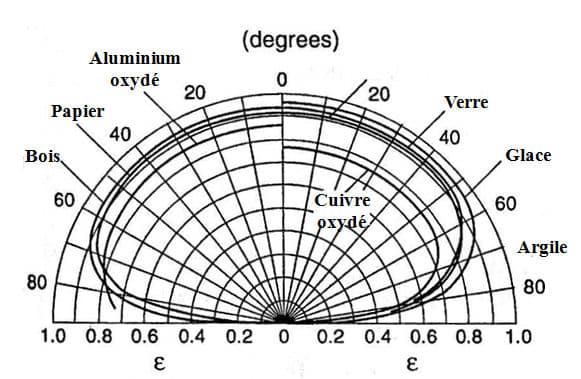
Abbildung 1

Gesamtemissionsgrad als Funktion der Richtung aus (1)

2. Berechnung der Emissivität aus dem komplexen Index

Das Gesetz der Energieerhaltung wird im Fall elektromagnetischer Strahlung durch das Kirchhoffsche Gesetz ausgedrückt. Im allgemeinen Fall verbindet dieses Gesetz für eine bestimmte Wellenlänge den Transmissionsfaktor, den hemisphärischen Richtungsreflexionsfaktor mit der Absorption, die in diesem Fall gleich der Emissivität ist.

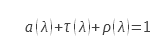
Dabei ist a der spektrale Absorptionsfaktor, τ der spektrale Transmissionsfaktor und ρ der hemisphärische Richtungsreflexionsfaktor.
Für ein undurchsichtiges Material lautet diese Beziehung

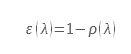
Da ε = a und für ein undurchsichtiges Material τ = 0.

Gleichung (8) ist die Grundlage aller indirekten Methoden zur Messung der Emissivität. Sie ermöglicht auch die Berechnung der Emissivität aus dem Reflexionsfaktor selbst, der nach den Fresnel-Beziehungen berechnet wird. Dieser Ansatz gilt nur für Dioptere, d. h. für glatte Oberflächen.

1.6 Berechnung der Emissivität für die beiden Polarisationen des Lichts

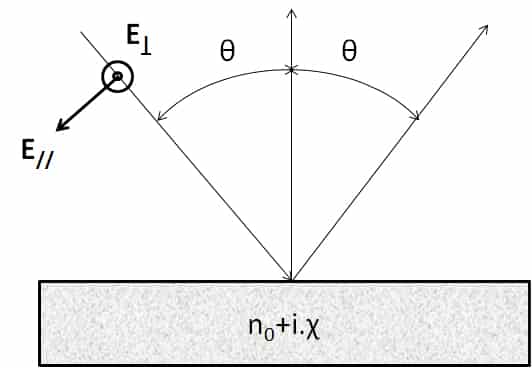
Für die planare Dioptrie kann man die Emissivität aus dem Ausdruck der Reflexionskoeffizienten berechnen, die aus dem komplexen Index n = n0+ i. χ berechnet werden. Diese detaillierte Berechnung findet sich in (2) aus den Maxwell-Gleichungen. Diese Ausdrücke werden aus den Fresnel-Koeffizienten für die Reflexion abgeleitet und sind in (3) zu finden. Die Gleichungen 9 und 10 können mit komplexen Indizes verwendet werden, wodurch sie für die Berechnung des Emissionsgrades von Metallen verwendet werden können. Überlegungen zu den Randbedingungen auf der Ebene der Dioptrie machen es notwendig, einen Reflexionskoeffizienten und damit einen Emissionsgrad für zwei unterschiedliche Polarisationen zu berechnen. Diese Polarisationen werden in der Abbildung in Abbildung 2 erläutert.

Abbildung 2

Spiegelreflexion auf einer ebenen Dioptrie

Für unpolarisiertes Licht müssen wir den arithmetischen Mittelwert der beiden Emissionsgrade bilden, die den beiden Polarisationen entsprechen. Die Ausdrücke der beiden Emissionsgrade für die beiden Polarisationen sind nachstehend aufgeführt :

Wir können sie in einer anderen Form schreiben :

Und

Wir können auch die normale Richtungsemissivität ε_n berechnen. In diesem Fall sind die beiden Polarisationen gleichwertig und wir erhalten für einen komplexen Index n das folgende Ergebnis:

1.7 Fall von Dielektrika

Abbildung 3 aus (2) zeigt die Richtungsemissivität als Funktion des Winkels für ein Dielektrikum mit einem Brechungsindex von 1,5: Dies entspricht einer relativen dielektrischen Permittivität von 2,25:

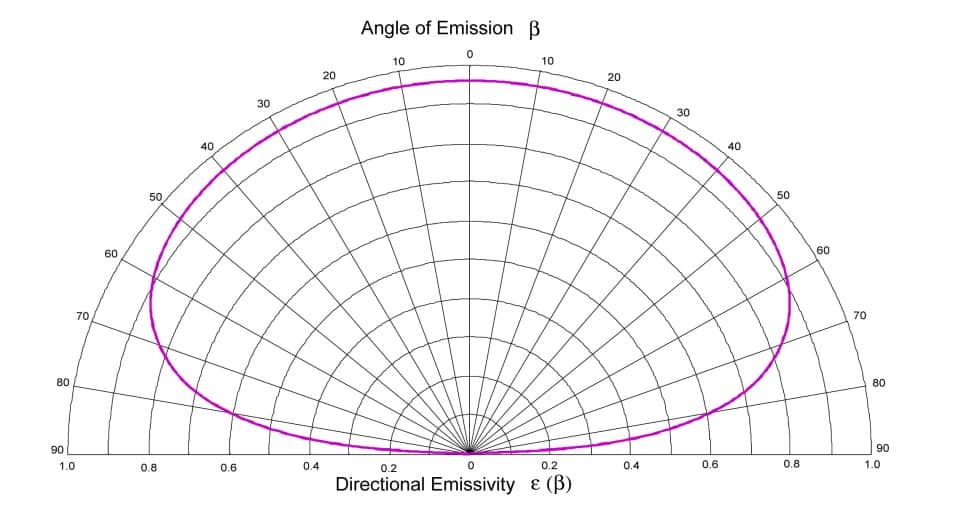
Abbildung 3

Richtungsabhängige Emissivität als Funktion des Winkels für ein Dielektrikum mit einem Brechungsindex von 1,5 (2)

Dies sind typische Eigenschaften von Glas auf Borosilikatbasis. Wir stellen fest, dass wir theoretisch denselben Emissionsgradindikator finden wie den experimentell gemessenen (Abbildung 1). Da der einzige Parameter, der den Emissionsgrad eines glatten dielektrischen Diopters verändern kann, der reale Brechungsindex ist, haben wir für einen gegebenen Brechungsindex immer denselben Emissionsgradindikator. Daher kann man durch Integration über die gesamte Hemisphäre den hemisphärischen Emissionsgrad berechnen.

Die Beziehung zwischen dem halbkugelförmigen Emissionsgrad und dem normalen Richtungsemissionsgrad ist daher nur eine Funktion des Brechungsindex und somit nur des normalen Richtungsemissionsgrades (Abbildung 1). Wir können daher die hemisphärische Emissivität aus der normalen Richtungsemissivität ableiten und umgekehrt. Diese Berichte sind in der Norm NF EN 12898 zur Bestimmung der Emissivität von Bauglas tabellarisch aufgeführt. Diese Studie kann für ein nicht glattes Dielektrikum mit einer guten Annäherung verwendet werden. Tatsächlich hat die Rauheit nur einen sehr geringen Einfluss auf den Emissivitätsindikator eines Dielektrikums. Diese Überlegungen werden in Abschnitt 2.4 aufgegriffen.

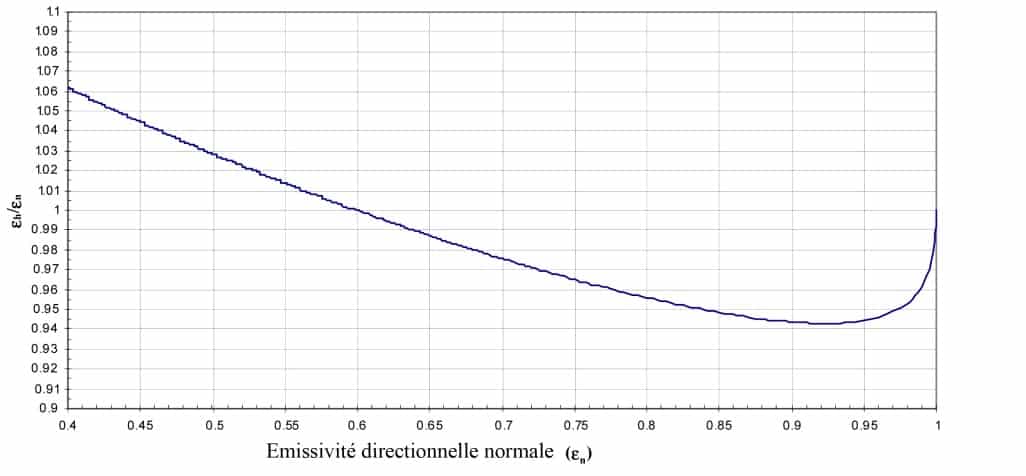
Abbildung 4

Beziehung zwischen der Emissivität der Hemisphäre und der Emissivität in Normalrichtung als Funktion der Emissivität in Normalrichtung für glatte Dielektrika (2)

1.8 Fall von Metallen und Leitern

Auf die gleiche Weise können wir den Emissionsgradindikator für einen Luft-/Metall-Diopter darstellen. Es ergibt sich ein theoretischer Emissionsgradindikator, der demjenigen ähnelt, der für ein Metall wie Aluminium ermittelt werden kann. Der in Abbildung 5 aus (2) dargestellte Wert wurde für einen für Metalle wie Aluminium typischen Brechungsindex berechnet: n = 5,7 + 9,7i. Die Entsprechung zwischen hemisphärischer Emissivität und normaler Richtungsemissivität besteht auch für Leiter, jedoch ist der Emissivitätsindikator unterschiedlich.

Daher ist es notwendig, die Leiter getrennt von den Dielektrika zu behandeln, um die Beziehung zwischen den beiden Emissivitäten zu bestimmen. Diese Studie kann nicht für einen nicht glatten Leiter verwendet werden. Tatsächlich hat die Rauheit einen starken Einfluss auf den Emissionsgradindikator eines Metalls, da der Emissionsgrad eines Metalls stark von dessen Rauheit abhängt. Eine detailliertere Studie zum Emissionsgrad von Metallen in Abhängigkeit von der Rauheit finden Sie in [30].

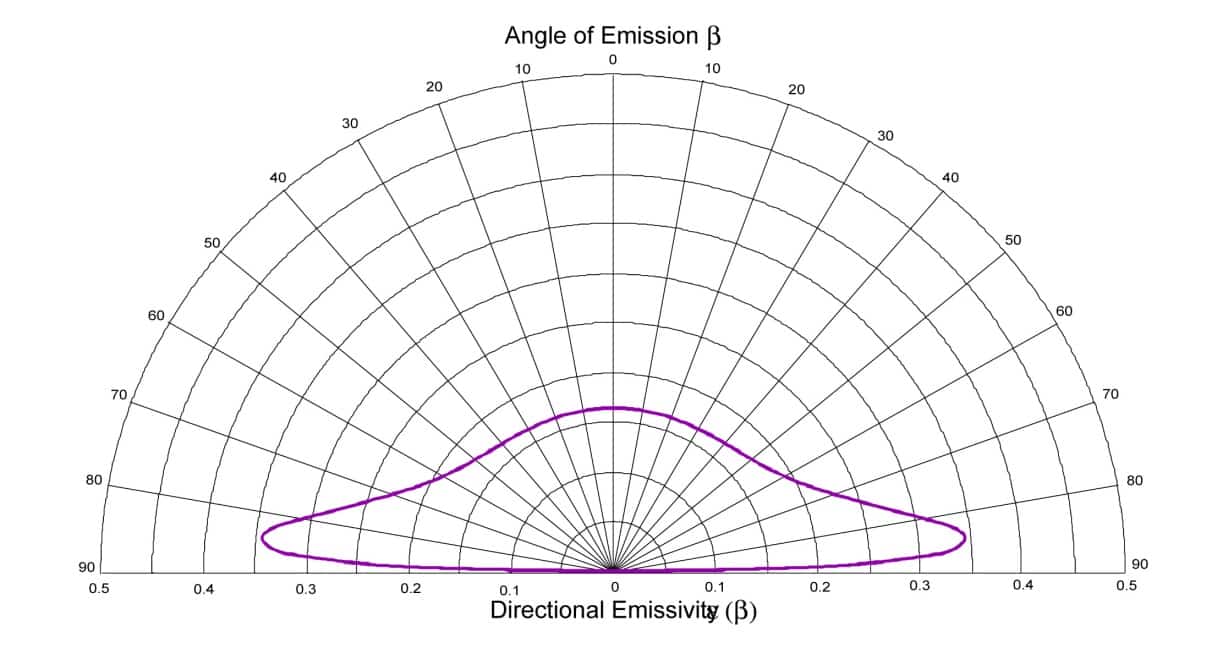
Abbildung 5

Richtungsabhängige Emissivität als Funktion des Winkels für ein Metall mit einem Brechungsindex von n = 5,7 + 9,7. i

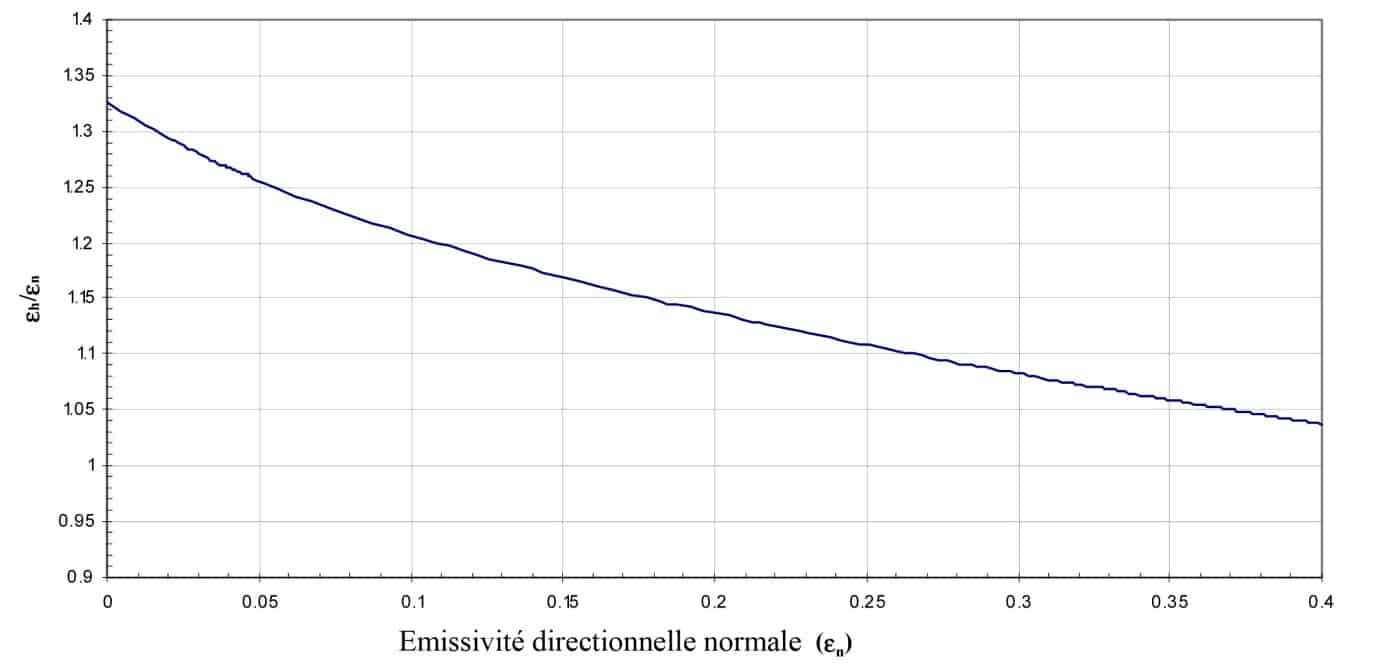
Abbildung 6

Beziehung zwischen der hemisphärischen Emissivität und der normalen Richtungsemissivität als Funktion der normalen Richtungsemissivität für glatte Leiter (2)

Bei Leitern können zwei Parameter, n0 und χ, variieren. Abbildung 6 zeigt eine theoretische Kurve, die durch Variation des Imaginärteils des Index erhalten wurde. Für komplexere Fälle und insbesondere für raue Oberflächen haben experimentelle Studien die Erstellung von Tabellenwerten ermöglicht.

1.9 Zusammenhang zwischen der normalen Richtungsemissivität und der hemisphärischen Emissivität

Aus Gründen der Einfachheit wird häufig die Richtungsemissivität bei nahezu normalem Einfall gemessen. Oftmals ist es jedoch erforderlich, die hemisphärische Emissivität zu ermitteln.

Dies ist die Integration der Richtungsemissivität über alle nutzbaren Raumwinkel. Wenn man diese nicht über den gesamten Einfallsbereich messen kann, muss man in der Lage sein, die hemisphärische Emissivität aus der Richtungsemissivität bei nahezu normalem Einfall abzuleiten. Diese Berechnung ist für glatte Dioptere aus Dielektrika theoretisch möglich, da die Emissivität nur vom Normalindex abhängt (Abbildung 1). Die Werte in Tabelle 1 stammen aus der ISO-Norm 12898. Sie ist für die Messung der Emissivität von Verglasungen vorgesehen.

Tabelle 1 Faktoren zur Berechnung der gesamten hemisphärischen Emissivität aus εn für eine glatte dielektrische Oberfläche

Einige bemerkenswerte Studien haben es ermöglicht, diesen Koeffizienten ε∩/ εn zu dokumentieren. Für glatte Oberflächen mit niedrigem Emissionsgrad (typischerweise Metalle) verwendeten Rubin und Hartmann (4) Silber und Inlayers2O3 auf Glas. Unter Verwendung experimenteller Daten und der Kramer-Kroning-Beziehungen wurde ein analytischer Ausdruck erhalten

Für Dielektrika, deren Emissivität εn zwischen 0,68 und 0,98 liegt, wird ein anderer Ausdruck verwendet (4) (5):

Diese Daten wurden in zwei europäischen Forschungsberichten (6) (7) zusammengefasst und ergänzt. Sie ermöglichten es, die für die Ausarbeitung der Norm ISO 12898 erforderlichen Daten bereitzustellen.
Diese Daten sind in Abbildung 7 dargestellt. Die Kurve „Metalle” entspricht der Gleichung (14), die Kurve „Dielektrika” der Gleichung (15). Die in ISO 13898 tabellarisch aufgeführten Werte sind ebenfalls in diesem Diagramm dargestellt.
.

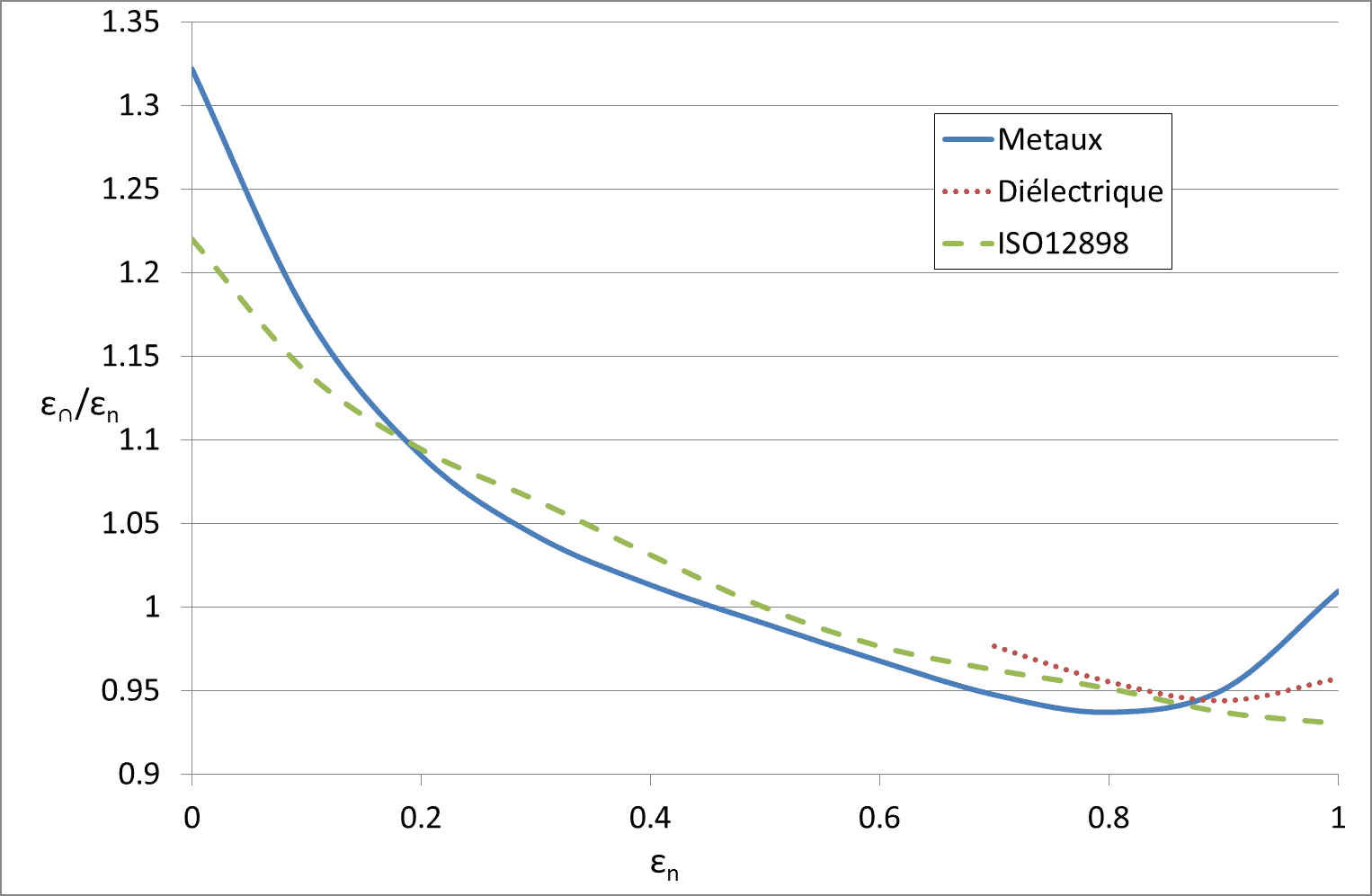
Abbildung 7

Beziehung zwischen ε und εn gemäß den verschiedenen Quellen

3 Die verschiedenen Methoden zur Messung der thermischen Emissivität

1.10 Klassifizierung der Methoden

In diesem Kapitel werden die Methoden zur Messung der Emissivität behandelt. Sie wurden nach dem physikalischen Messprinzip klassifiziert. Wir haben die sogenannten direkten Methoden von den sogenannten indirekten Methoden getrennt. Direkte Methoden sind solche, bei denen die von der Oberfläche abgestrahlte Leistung direkt gemessen wird: Dies sind kalorimetrische und radiometrische Methoden.
Indirekte Methoden sind solche, bei denen die Eigenschaften von Oberflächen im infraroten Spektralbereich durch Reflektometrie aus den optischen Eigenschaften abgeleitet werden: Dies ist bei allen anderen Methoden der Fall. Alle kommerziellen Geräte verwenden diese indirekten Methoden in der einen oder anderen Form. Die direkten Methoden sind nur durch das verwendete Versuchsetzteil begrenzt. Indirekte Methoden leiden unter intrinsischen Verzerrungen in der Messmethode selbst.

1.11 Kalorimetrische Methode

Mit dieser Methode lassen sich Strahlungstransfers bewerten, ohne dass dabei bestimmte Einfallswinkel oder Wellenlängen vernachlässigt werden. Sie besteht darin, eine Energiebilanz der Strahlungsverluste der untersuchten Probe zu erstellen, wenn nur diese Verluste eine Rolle spielen. Es handelt sich um eine direkte und absolute Methode, d. h. es ist kein Referenzstandard für die Emissivität erforderlich, um
die Emissivität der Probe zu ermitteln. Diese Methode ist jedoch nach wie vor aufwendig. Um Übertragungen durch Wärmeleitung und Konvektion zu eliminieren, muss die Probe unter einer reduzierten Atmosphäre (typischerweise 10−5 mbar) platziert werden. Die Probe wird erhitzt und auf der Temperatur gehalten, bei der das Emissionsvermögen ermittelt werden soll. Um ihre Temperatur aufrechtzuerhalten, muss sie mit
Energie versorgt werden :

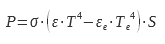
wobei P die von der Probe abgegebene Leistung, ε ihr Emissionsgrad, σ die Stefan-Boltzmann-Konstante, T die Temperatur der Probe, εe der Emissionsgrad des Gehäuses, Te die Temperatur des Gehäuses und S die Emissionsfläche der Probe ist. Die Leistung, die erforderlich ist, um die Probe auf der Temperatur zu halten, bei der der Emissionsgrad ermittelt werden soll, wird in Form des Joule-Effekts elektrisch zugeführt. Abbildung 8 zeigt schematisch eine Vorrichtung zur Messung des Emissionsgrades nach der kalorimetrischen Methode. Das Gehäuse (F) wird mit Hilfe einer Pumpvorrichtung, die über die Rohrleitung A mit dem Gehäuse verbunden ist, unter Vakuum gehalten.

Die Stromversorgungs- und Messleitungen (B) sind über einen Anschlussblock C mit der Probe verbunden. Dieser dient als Schutz, um Verluste durch Wärmeleitung zu vermeiden. Die Temperatur dieses Anschlussblocks wird auf derselben Temperatur wie die Probe gehalten und geregelt. Auf diese Weise ist die durch Wärmeleitung über die Stromversorgungs- und Messleitungen zwischen dem Anschlussblock und der Probe abgegebene Leistung aufgrund des fehlenden Temperaturgradienten gleich Null. Die Probenscheibe mit bekannter Strahlungsfläche ist in der Umhüllung aufgehängt. Die Umhüllung E ist ein thermisch isolierter Kryostat, der in der Regel mit flüssigem Stickstoff gefüllt ist. Helium wird verwendet, wenn Emissionsgrade bei niedrigen Temperaturen (unter 250 K) für die Raumfahrtindustrie gemessen werden sollen. Eine solche Vorrichtung ist in (8) beschrieben. Das Gehäuse F ist innen mit einer Beschichtung mit hohem Emissionsgrad und spektralem Emissionsgrad versehen, der sich mit der Wellenlänge nur wenig ändert. Die Wahl der Kryostattemperatur richtet sich nach der Notwendigkeit, dass ε.T4 ≫ εe.Te4 sein muss. Die ideale Temperatur sollte eine Vorspannung ermöglichen, die viel geringer ist als die Messunsicherheit des Geräts. Aus Beziehung 16 können wir den Emissionsgrad ableiten :

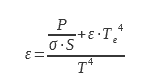
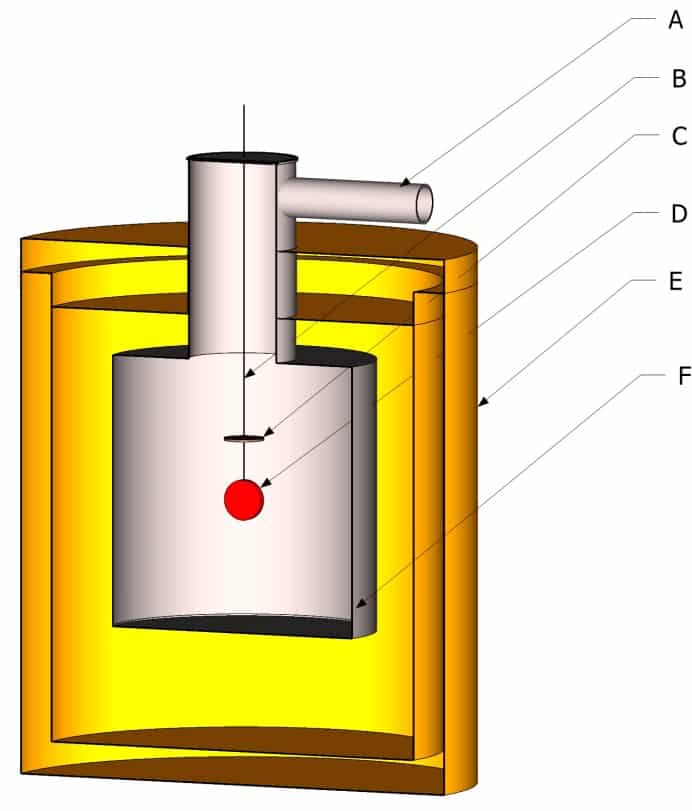
Abbildung 8

Schematische Darstellung der kalorimetrischen Methode

Die kalorimetrische Methode ist die einzige, die eine direkte Bestimmung der gesamten hemisphärischen Emissivität ermöglicht. Dabei wird die gesamte Strahlung berücksichtigt. Da sie keine Referenz oder einen Emissivitätsstandard erfordert, gilt sie als Referenzmethode. Allerdings ist diese Methode nach wie vor umständlich und zeitaufwendig in der Anwendung. Es wäre schwierig, mit dieser Methode allein eine Emissivitätsdatenbank aufzubauen.

Die größte Unsicherheit besteht bei der Messung der Oberflächentemperatur. Diese kann durch Messung des Temperaturgradienten im Inneren der Probe mit verschiedenen Sensoren extrapoliert werden (9). Außerdem müssen die Proben in ihrer Größe so kalibriert sein, dass sie in das Messgerät passen. Andere, einfachere Geräte werden in (10) beschrieben.

1.12 Radiometrische Methode

1.1.1 Methode durch direkte Messung des Flusses/der Leuchtdichte

Diese Methode besteht darin, die Leuchtdichte einer Probe mit der eines auf die gleiche Temperatur gebrachtem schwarzen Körpers zu vergleichen. Das Gerät ist in Abbildung 9 dargestellt. In dieser Abbildung wird die Probe A auf die Temperatur gebracht, bei der die Emissivität gemessen werden soll. Diese wird in eine gekühlte Kammer B mit den gleichen Temperaturbedingungen wie bei der kalorimetrischen Methode (ε.T4 ≫ εe.Te4) gebracht. Ein auf die gleiche Temperatur wie die Probe gebrachtes Schwarzkörper E dient als Leuchtdichte-Referenz. Die Leuchtdichte des schwarzen Körpers und die der Probe werden nacheinander mit Hilfe des Kippspiegels C gemessen. Das Verhältnis zwischen diesen beiden Leuchtdichten ergibt den Emissionsgrad. Der schwarze Körper wird in einem isolierten Gehäuse ohne Temperaturbedingungen platziert. Es ist möglich, die Messung mit einem schwarzen Körper durchzuführen, dessen Temperatur sich von der der Probe unterscheidet. In diesem Fall gilt ein Verhältnis zwischen den Temperaturen mit der Potenz 4.

Die beiden Leuchtdichten werden mit dem Detektor D gemessen. Dabei kann es sich um einen Breitband-Infrarotdetektor (wie eine Thermosäule) handeln, um die Gesamtemissivität zu messen. Dieser Detektor kann mit einem Filterrad ausgestattet werden, um die spektrale Emissivität für verschiedene Wellenlängen zu messen (11). Die Geräte zur Messung der Emissivität durch Vergleich mit einem schwarzen Körper vom NIST (National Institute of Standards and Technology, Gaithersburg, Maryland, Vereinigte Staaten) sind in (12) vorgestellt. In diesem Gerät gibt es keinen Kippspiegel, das Detektionssystem wird mittels eines Schlittens vor die zu messenden Oberflächen und die Referenzschwarzkörper bewegt. Dieses Gerät ist ein Maßstab auf dem Gebiet der Emissionsgradmessungen für Temperaturen von 600 K bis 1400 K. Das in (13) beschriebene Emissionsmessgerät verwendet ein Fourier-Transform-Infrarotspektrometer. Die Leuchtdichte wird daher nur in einer Richtung gemessen, es wird also eine gerichtete Emissivität gemessen. Um verschiedene Einfallswinkel zu messen und zur hemisphärischen Emissivität zurückzukehren, ermöglichen bestimmte Geräte die Drehung der Probe: Dies ist bei dem in (13) beschriebenen Gerät der Fall. Das Spektrometer kann auch durch einen Monochromator ersetzt werden, wie das in (14) beschriebene Gerät.

Die radiometrische Messung bei Raumtemperatur erfordert die Platzierung der Probe in einem Kryostaten bei sehr niedriger Temperatur und unter Vakuum, um Kondensation zu vermeiden. Ein originelles Gerät, das dieses Problem umgeht, wird in (15) beschrieben. Das Prinzip bleibt dasselbe, jedoch werden die Messungen bei Raumtemperatur durchgeführt, der gemessene Fluss wird dann anhand der Temperaturmessungen des Gehäuses und des Choppers korrigiert. Dies vereinfacht das Gerät erheblich, führt jedoch zu zusätzlichen Unsicherheitsquellen.

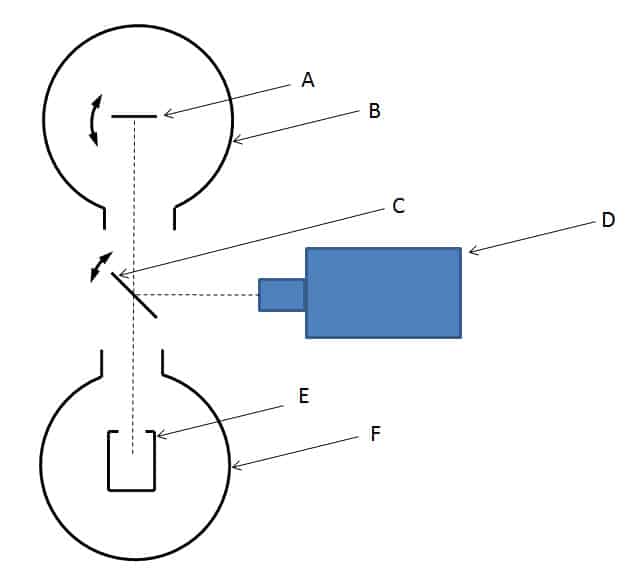
Abbildung 9

Radiometrische Methode

Das Verfahren besteht darin, die Temperatur der Probe geringfügig um die Temperatur herum zu modulieren, bei der man den Emissionsgrad ermitteln möchte. Auf diese Weise können wir den reflektierten Fluss vom eigenen Fluss der Probe trennen. Dies ist das Prinzip der modulierten radiometrischen Methode.

Um die Emissivität zu ermitteln, muss der gemessene Fluss mit dem einer Oberfläche mit bekannter Emissivität verglichen werden. Eine andere Methode besteht darin, zusätzlich eine halbkugelförmige Quelle mit einer anderen Frequenz als der Modulationsfrequenz der Probe zu modulieren. Durch die Messung an zwei unbekannten Proben lassen sich der Wert der Emissivität und der Reflektivität ermitteln. Bei dieser Methode ist für die Messung keine Emissivitätsreferenz erforderlich. Die periodische radiometrische Methode wird in [20] ausführlich beschrieben.

1.13 Reflektometrische Methoden

Die reflektometrische Methode besteht darin, den hemisphärischen Richtungsreflexionskoeffizienten ρ^(∩ |) oder den hemisphärischen Richtungsreflexionskoeffizienten ρ^(| ∩ in) zu messen, um die Richtungsemissivität für eine Richtung zu berechnen, die der zur Messung des Reflexionskoeffizienten verwendeten Richtung entspricht. Diese Berechnung basiert auf dem Kirchhoffschen Gesetz (2). Dieses Gesetz lässt sich wie folgt formulieren: Für eine undurchsichtige Oberfläche, die sich im thermischen Gleichgewicht mit ihrer Umgebung befindet, gilt für eine Wellenlänge λ :

Das thermische Gleichgewicht bedingt eine identische Temperatur für die Umgebung und die betreffende Oberfläche. Diese Beziehung lässt sich auf einen Wellenlängenbereich ausweiten.

Dieser Reflexionskoeffizient kann entweder durch Messung der Reflexion für alle Wellenlängen und durch Durchführung der Integration, gewichtet mit der Emittanz des schwarzen Körpers, oder durch Sicherstellung, dass die Reflexion mit einer Lichtquelle gemessen wird, berechnet werden. die die gleiche spektrale Energieverteilung wie der schwarze Körper bei der betrachteten Temperatur aufweist. Es muss auch sichergestellt werden, dass der verwendete Infrarotdetektor im betrachteten Spektralbereich eine ausreichend konstante Empfindlichkeit aufweist. Sofern die spektrale Reflexion nicht mit der Temperatur variiert, kann man diese Reflexion berechnen, ohne sich um die Temperatur der Probe zu kümmern. Wir werden mehrere Methoden zur Messung der Emissivität anhand der Reflexionsmessung betrachten.

Abbildung 10

Schematische Darstellung eines Geräts zur Messung der hemisphärischen Richtungsreflexion unter Verwendung der Ulbrichtkugelmethode

1.1.3 Integralkugelmethode

Abbildung 10 zeigt die Funktionsweise einer Integrationskugel. Diese muss innen mit einer reflektierenden und streuenden Beschichtung versehen sein. Die Probe wird von einer Infrarotquelle in einer bestimmten Richtung nahe der Normalen beleuchtet. Der Einfallswinkel in den handelsüblichen Integrationskugeln liegt zwischen 8 und 12 Grad. Sobald das Licht die Probe erreicht hat, wird es entsprechend dem Reflexionsgrad des Materials in alle Richtungen gestreut. Nach mehreren Reflexionen erreicht das Licht den seitlich angebrachten Detektor. Somit misst der Detektor theoretisch fast den gesamten von der Probe reflektierten Lichtstrom.

Ein Blenden-System verhindert, dass der Detektor die Probe direkt sieht, um die Messung nicht zu stören. Ein Detektor kann symmetrisch zur Quelle platziert werden, um die Spiegelreflexion zu messen. Dieser ist optional, und bei bestimmten Kugeln kann man an der Stelle der Spiegelreflexion entweder einen Teil der diffusen Oberfläche derselben Art wie die Kugel anbringen oder sie offen lassen. Im ersten Fall wird der gesamte reflektierte Lichtstrom (diffus und spiegelnd) gemessen, im anderen Fall nur der diffuse Lichtstrom.

Durch Subtraktion kann der Spiegelreflexionskoeffizient ermittelt werden. Um eine Reflektionskoeffizientenmessung durchzuführen, muss das Gerät mit einer Reflexionsreferenz kalibriert werden. Es wird die gleiche Art von Beschichtung verwendet wie für die Kugel. In der Regel handelt es sich um eine geschliffene Metalloberfläche, die mit einer Goldschicht überzogen ist. Ein Gerät dieser Art wird am NIST verwendet. Es wird in (16) beschrieben.

1.1.4 Methode unter Verwendung einer modulierten Quelle

Bisher mussten wir bei der radiometrischen Methode, wenn wir den von der Oberfläche emittierten Fluss messen wollten, den Fluss aus der Strahlungsumgebung um die Probe herum eliminieren. Diese wurde daher in eine auf eine Temperatur Te gekühlte Umhüllung gebracht, um sicherzustellen, dass σ.T4>> σ.Te4. Diese einschränkende Bedingung ist jedoch dank eines wassergekühlten Gehäuses für Probentemperaturen in der Größenordnung von 1000 K leicht zu erreichen. Wenn man jedoch eine Emissivität bei Raumtemperatur messen möchte, muss das Gehäuse auf kryogene Temperaturen gekühlt werden. Um diese zusätzliche Komplexität zu vermeiden, kann die Temperatur der zu messenden Probe um die Temperatur herum moduliert werden, bei der die Emissivität gewünscht ist (17). In diesem Fall wird der modulierte emittierte Fluss erfasst und mit einer Modulationsamplitude verglichen, die der von einer Referenzfläche emittierten entspricht. Wenn es nicht möglich ist, die Temperatur der Probe zu modulieren, kann eine reflektometrische Methode verwendet werden, und der zur Messung des Reflexionsfaktors verwendete Fluss kann moduliert werden. Diese Methoden werden in (18) beschrieben, und ein konkretes Anwendungsbeispiel findet sich in (19).

Um den eigenen Fluss der Probe vom reflektierten Fluss zu trennen, wird ein frequenzmodulierter halbkugelförmiger Fluss darüber gesendet. Das Prinzip besteht darin, einen halbkugelförmigen Infrarotfluss zu erzeugen, der um die untersuchte Probe herum moduliert wird, und in einer Richtung den von der Oberfläche des Materials reflektierten Fluss mit einer Thermosäule zu messen. Das Diagramm in Abbildung 11 zeigt das Prinzip des Geräts. Das Gerät wird zuvor mit einem bekannten Referenzmaterial kalibriert. Abbildung 12 zeigt das Schema des bei CERTES (19) entwickelten Geräts sowie ein Foto des Instruments. Der Hohlraum besteht aus einem hohlen Aluminiumwürfel, der nach unten offen ist. Die Temperatur der Wände wird mit Peltier-Elementen moduliert. Die Messung des reflektierten Flusses erfolgt durch eine Öffnung an der Oberseite des Geräts mittels einer Thermosäule, die mit einer KRS5-Linse ausgestattet ist.

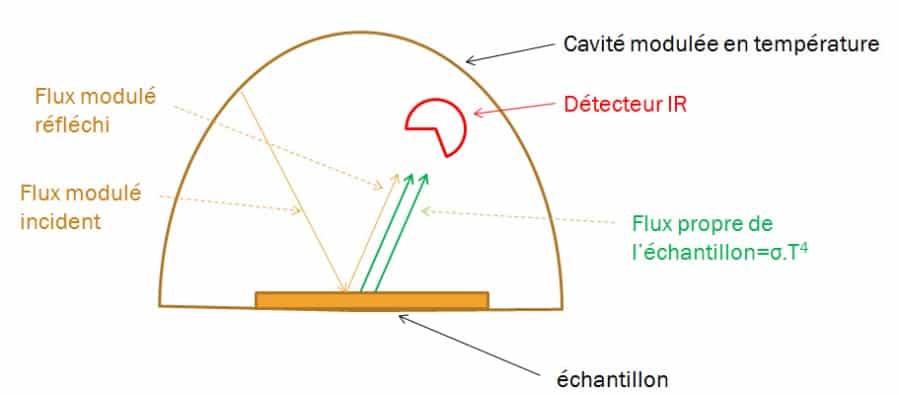
Abbildung 11

Prinzip der reflektometrischen Messmethode mit einer modulierten Quelle

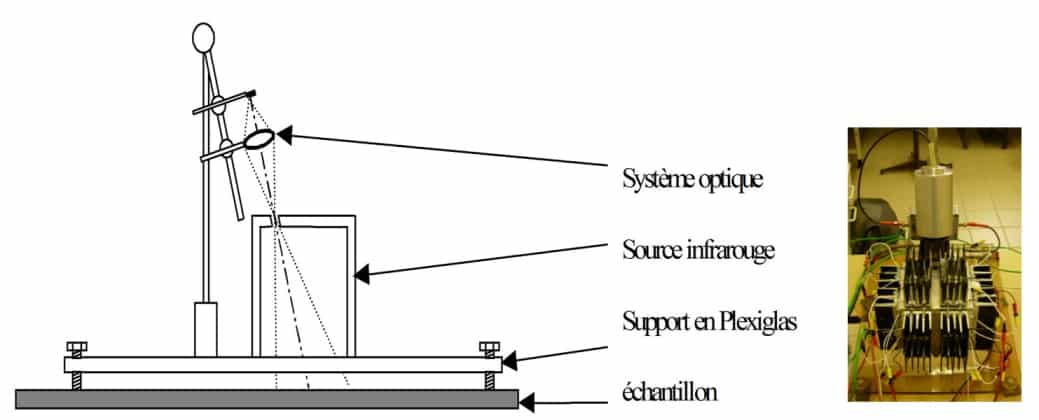
Abbildung 12

Diagramm und Foto des bei CERTES entwickelten Messgeräts

Eine weitere Methode zur Modulation des hemisphärischen Flusses ist die Verwendung eines dreidimensionalen Choppers. Dieses Gerät wurde von der Universität Paris XII patentiert. Das Gerät wird im Folgenden vorgestellt.

EM3 von THEMACS Engineering:

Das Prinzip dieses Geräts entspricht dem oben beschriebenen. Es besteht darin, eine halbkugelförmige Strahlungsquelle durch bewegliche Klappen zu modulieren. Dadurch wird eine Modulation des Temperaturhohlraums vermieden, die sehr langsam ist. Das Diagramm in Abbildung 21 zeigt das Prinzip der Modulation.
Die Quelle ist der Zylinder B, der auf eine Temperatur leicht über der Umgebungstemperatur erhitzt wird. Der bewegliche Zylinder C und die feste Blende D verdecken die halbkugelförmige Quelle mit einer Frequenz von 10 Hz für die zylindrische Wand (6 Fenster) und 5 Hz für den oberen Teil (3 Fenster). Auf diese Weise ist es möglich, ein spiegelndes Material von einem streuenden Material zu unterscheiden. Eine Thermosäule misst den einfallenden Fluss und eine andere den reflektierten Fluss. Das Verhältnis des reflektierten Flusses hängt nicht von der von der Quelle emittierten Intensität ab.

Dieses Emissometer muss zuvor mit zwei Oberflächen mit bekannter Emissivität kalibriert werden. In der Regel verwenden wir eine Oberfläche mit sehr hoher Emissivität (Nextel-Farbe, 3M ™) und eine Oberfläche mit sehr geringer Emissivität (diffus reflektierendes Aluminium). Abbildung 21 zeigt das allgemeine Schema (1), eine Detailansicht der beweglichen und festen Blenden sowie der mit Nextel-Farbe (3M™) beschichteten Quelle (2), eine Explosionsdarstellung des Geräts (3) und ein Foto des Geräts. Das Gerät ist tragbar und muss an einen Computer angeschlossen werden, der die Demodulation der Signale mittels FFT ermöglicht.

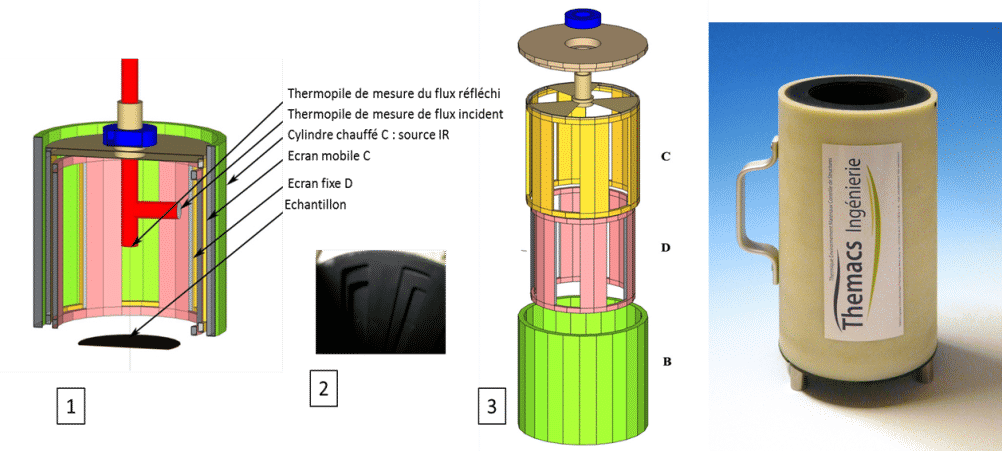
Abbildung 13

EM3-Emissionsmessgerät von THEMACS Engineering

4 Weiterführende Informationen

Mehrere allgemeine Dokumente können diese Studie über Emissionsgradmessungen ergänzen. Dazu gehören:
– „Measurement of Thermal Radiation Properties of Solids” (Messung der Wärmestrahlungseigenschaften von Feststoffen), [13]. Dieses Dokument enthält die Beiträge eines Kongresses aus dem Jahr 1962 über die Strahlungseigenschaften von Materialien. Trotz des Alters dieser Veröffentlichung listet sie umfassend eine große Anzahl von Emissionsgradmessgeräten auf, die in der Luftfahrt eingesetzt werden. Auch wenn sich die Technologien seitdem stark weiterentwickelt haben, sind die Messprinzipien dieser Geräte nach wie vor aktuell.
– „Measurement Techniques for Thermal Radiation Properties” (Messtechniken für thermische Strahlungseigenschaften), [12]. In ähnlicher Weise gibt dieses Dokument einen Überblick über den Stand der Technik im Jahr 1990. Es werden neue Geräte beschrieben.

– „Spacecraft Thermal Control Coatings References” (Referenzen zu thermischen Kontrollbeschichtungen für Raumfahrzeuge), [11]. Dieses Referenzdokument der NASA, eines der aktuellsten, beschreibt zunächst die gemessenen Größen. Anschließend wird eine theoretische Berechnung vorgestellt, die die komplexen Indizes der Materialien und die Strahlungseigenschaften miteinander verknüpft. Danach werden die verschiedenen Messmethoden beschrieben. Am Ende des Dokuments werden Messungen an Materialien vorgestellt, die häufig in der Luft- und Raumfahrt verwendet werden. Dieses Dokument beschreibt, wie das oben zitierte erste Dokument, auch die optischen Eigenschaften im sichtbaren Bereich; diese sind ebenfalls wichtig, um die Wärmebilanz eines der Sonnenstrahlung ausgesetzten Satelliten abzuleiten.

5 Bibliography

Maldague, X.P. Theorie und Praxis der Infrarottechnologie für zerstörungsfreie Prüfungen. s.l.: Ed. Wiley, 2001.
Kauder, L. Referenzen zu thermischen Kontrollbeschichtungen für Raumfahrzeuge, NASA-TP-2005-212792. 2005.
P. Lorrain, D.R. Corson. Champs et ondes électromagnétiques. s.l. : Armand Collin.
Rubin, M., Arasteh, D. und Hartmann, J. Eine Korrelation zwischen normaler und hemisphärischer Emissivität von Beschichtungen mit niedrigem Emissionsgrad auf Glas. s.l. : Int. Comm. Heat Mass Transfer, 1987.
Blain, B. J. und Douglas, R. W. Infrarotoptische Konstanten von Gläsern. 1965.
D. Janssen, J. Lohrengel. Untersuchung und Entwicklung einer Methode zur Messung der Emissivität von Glas. s.l. : BCR Europäische Gemeinschaft, 1991. EUR 13487 EN.
GEOTTI-BIANCHINI, F. Gesamtes hemisphärisches Emissionsvermögen von beschichtetem Glas. s.l. : Europäische Gemeinschaft, 1993. EUR 14758 EN.
C. Fabron, A. Meurat. Messung des gesamten hemisphärischen Emissionsvermögens bei niedrigen Temperaturen. s.l. : Internationales Symposium über Umweltprüfungen für Raumfahrtprogramme, Lüttich, Belgien, 2001.
J. Hameury, B. Hay, J. R. Filtz. Messung der gesamten hemisphärischen Emissivität unter Verwendung von. s.l. : Int. J. Thermophys, 1607, 2007.
S. Moghaddam, J. Lawler, J. Currano. Neuartige Methode zur Messung der gesamten hemisphärischen Emissivität. s.l. : J. Thermophys. Heat Transfer, 2007.
A. Mazikowski, K .Chrzanowski. Berührungsloses Multiband-Verfahren zur Emissivitätsmessung. s.l. : Infrared Phys. Technol., 91, 2003.
L. Hanssen, S. Mekhontsev, V. Khromchenko. Einrichtung zur Charakterisierung der infraroten spektralen Emissivität am NIST, . s.l. : Thermosense XXVI, herausgegeben von Douglas D. Burleigh, K. Elliott Cramer, G. Raymond Peacock, Proc. of SPIE Vol. 5405, SPIE, Bellingham, WA, 2004.
L. Del Campo, R.B. Perez-Saez, X. Esquisabel, I. Fernandez, M.J. Tello. Neues experimentelles Gerät zur Messung der spektralen Richtungsemissivität im Infrarotbereich in einer kontrollierten Umgebung. s.l. : Review Of Scientific Instruments, Band 77, 113111, 1-8, 2006.
V. Vitkovskii, V. G. Gorshenev, Y. F. Potapov. Messung der spektralen Richtungsemissivität von Materialien und Beschichtungen im Infrarotbereich des Spektrums. s.l. : Thermal Engineer , 245-248 Vol. 56-3, 2009.
A. Pantinakis, N. Kortsalioudakis. Ein einfaches hochempfindliches Radiometer im Infrarotbereich zur Messung der gerichteten Gesamtemissivität opaker Materialien bei Temperaturen nahe der Umgebungstemperatur. s.l. : International Journal of Thermophysics, 1843-1854 Vol. 22-6, 2001.
L.M. Hanssen, S. Kaplan. Infrarot-Diffusreflexionsmessgeräte und -Standards am NIST. s.l. : Anal. Chim. Acta, 289 , 1999.
D. Especel, S. Matteï. Messung der Gesamtemissivität ohne Verwendung einer absoluten Referenz. s.l. : Infrared Phys. Technol., 777-784 Band 37, 1996.
L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau. Infrarot-Emissionsgradmessgerät: Prinzip und Anwendungen. s.l.: Meas. Sc. Tech., 2950, 2006.
M. Siroux. Entwicklung von Techniken zur Messung des Emissionsgrades undurchsichtiger Materialien bei Raumtemperatur. Radiometrische und kalorimetrische Ansätze im periodischen Betrieb. s.l.: Dissertation Universität Paris 12, 1996.

Nuestro equipo le asesora para satisfacer mejor sus expectativas.

Contáctenos