Importancia y limitaciones de las mediciones espectrales
Importancia y limitaciones de las mediciones espectrales para la medición de la emisividad
Autores :
Jean-Pierre MONCHAU, THEMACS Ingénierie, 2bis rue Alfred Nobel, 77420 Champs sur Marne,monchau@themacs.fr
Laurent IBOS, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, ibos@u-pec.fr
Mario MARCHETTI, CEREMA, Laboratoire Régional de Nancy,71, rue de la Grande Haie – 54510 Tomblaine,Mario. Marchetti@cerema.fr
Jean DUMOULIN, IFSTTAR, Dépt. CoSys, Route de Bouaye, 44344 Bouguenais Cedex, jean.dumoulin@ifsttar.fr
Vincent FEUILLET, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, vincent.feuillet@u-pec.fr
Emisividad
La emisividad es una propiedad termofísica de los materiales importante para cuantificar el intercambio de calor por radiación. También es esencial para medir la temperatura superficial a partir de una medición de luminancia, como por ejemplo mediante termografía infrarroja.
Esta última técnica se está generalizando con la democratización de las cámaras térmicas con matrices de microbolómetros. La medición de la emisividad a temperatura ambiente se realiza generalmente mediante el método indirecto, utilizando la ley de Kirchhoff que relaciona la emisividad con la reflectancia de un material opaco. Existen varios dispositivos comerciales, pero estos dispositivos tienen sesgos de medición. Para corregir estos defectos, es necesario conocer el comportamiento espectral del material.
La medición del factor de reflexión espectral con un espectrómetro infrarrojo por transformada de Fourier (FTIR) equipado con una esfera integradora permite obtener esta información. Sin embargo, la limitación espectral de las esferas integradoras (generalmente 1-20 µm) hace necesario un emisímetro que cubra un rango espectral más amplio.
Definición de emisividad
Max Planck determinó teóricamente la emisividad espectral de un cuerpo ideal denominado cuerpo negro utilizando la teoría cuántica (Figura 1). Las superficies reales irradian de forma similar, pero la emisividad se pondera mediante un coeficiente adimensional denominado emisividad.
Este coeficiente depende del material, su temperatura, la longitud de onda y la incidencia (en este caso, el ángulo de emisión). Los ingenieros térmicos prefieren utilizar un coeficiente integrado en todo el espectro y para todas las incidencias, denominado emisividad hemisférica total, con el fin de poder cuantificar, por ejemplo, la cantidad de calor que pierde una superficie por radiación.
La dificultad radica, por tanto, en determinar este coeficiente sin descuidar las longitudes de onda ni las incidencias.
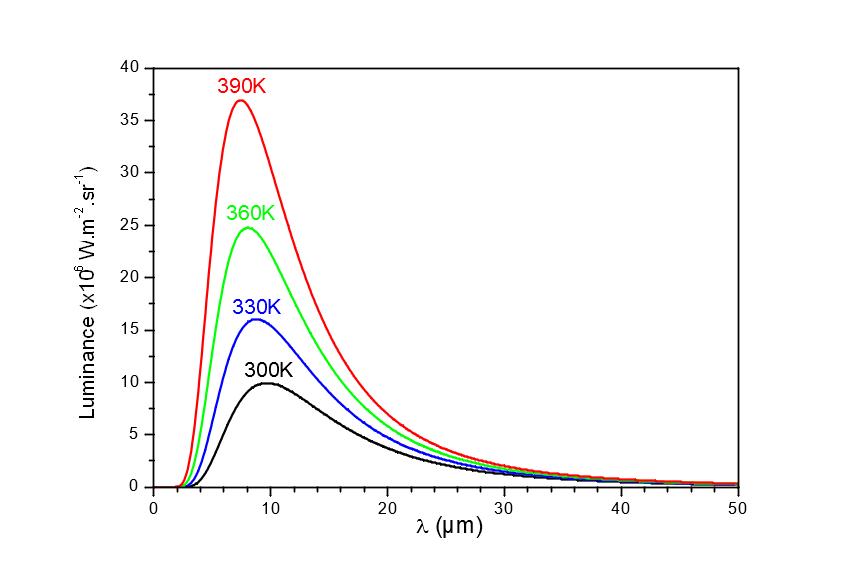
Figura 1
Luminancia de un cuerpo negro L(λ) para diferentes temperaturas T
Para medir la emisividad existen muchos enfoques que podemos clasificar en dos categorías: los métodos directos miden la radiación energética de la superficie estudiada y los métodos indirectos deducen la emisividad a partir de otras propiedades ópticas de la superficie.
Entre los métodos directos, cabe citar el método calorimétrico, que consiste en medir la potencia eléctrica que se debe suministrar a una muestra (colocada en un criostato al vacío) para mantener su temperatura superficial igual a la temperatura a la que se desea conocer la emisividad. El Laboratorio Nacional de Metrología y Ensayos (LNE) dispone de un banco de medición de este tipo [3].
Otro método, denominado radiométrico, consiste en medir la radiación térmica procedente de la superficie del material. Esta medición puede realizarse en función del ángulo para obtener la emisividad direccional y en función de la longitud de onda (con un espectrómetro FTIR, por ejemplo) para obtener la emisividad espectral direccional. El dispositivo CEMHTI (Condiciones Extremas y Materiales y Radiación a Alta Temperatura) permite este tipo de medición a temperaturas muy elevadas [4].
Para medir la emisividad a temperatura ambiente, el nivel del flujo es demasiado bajo para poder medirlo con precisión: este es el ámbito privilegiado de los métodos indirectos. Estos utilizan la ley de Kirchhoff, que relaciona la emisividad ε con la reflectancia ρ y la transmitancia τ para una longitud de onda λ dada :
![]()
la emisividad es igual a la absorción. Por lo tanto, para un material opaco, la emisividad es igual a :
![]()
Para obtener la emisividad total, debemos sumar el factor de reflexión espectral (es la primera vez que veo esta palabra) ponderado por la distribución espectral de energía del cuerpo negro a la temperatura a la que se desea conocer la emisividad :
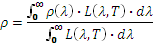
La otra solución consiste en medir el factor de reflexión global iluminando la superficie con una fuente de luz que tenga esta distribución de energía.
Varios dispositivos comerciales que miden la emisividad utilizan este método. Su principal cualidad es que miden la reflectancia en una banda espectral que va de 1 a 50 µm, lo que representa el 95 % de la energía irradiada por un cuerpo negro a temperatura ambiente (alrededor de 300 K). Sin embargo, integran el factor de reflexión para una distribución espectral diferente de la temperatura ambiente.
De hecho, utilizan cuerpos negros o grises como fuentes de infrarrojos a una temperatura superior a la temperatura ambiente. Estas fuentes tienen distribuciones espectrales diferentes a las de un cuerpo negro a 300 K. Esta diferencia en la distribución espectral da lugar a errores de medición de la emisividad de hasta un 5 % para los cuerpos que no son grises. Este defecto no es nada nuevo.
De hecho, la norma ASTM E408-71 (Método de ensayo estándar para la emisividad normal total de una superficie utilizando técnicas de medición por inspección) lo afirma. También podemos remitirnos a [5], donde se menciona brevemente este tipo de error.
Los emisómetros desarrollados en CERTES [1,2] utilizan fuentes infrarrojas moduladas en temperatura a temperaturas muy cercanas a la temperatura ambiente. El problema sigue sin resolverse porque la modulación afecta significativamente a la distribución espectral de la fuente (véase el recuadro 1).
Para eliminar esta incertidumbre, es necesario medir la reflectancia espectral direccional hemisférica (que es igual a la reflectancia direccional hemisférica por razones de reciprocidad). Los únicos dispositivos comerciales que permiten realizar esta medición son las esferas integradoras. Se pueden acoplar a espectrómetros FTIR y permiten realizar mediciones en la banda espectral de 1-20 µm.
Lo que hoy en día limita el rango espectral de las esferas integradoras comerciales, es el revestimiento interior de estas. Debe ser perfectamente difusor (comportamiento lambertiano). Esto ya no es así para longitudes de onda superiores a 20 µm. Por lo tanto, debemos conformarnos con esta banda espectral, que representa solo el 76 % de la energía radiada a 300 K. El dispositivo utilizado en CERTES y por THEMACS Engineering es un espectrómetro infrarrojo con transformada de Fourier FRONTIER© de la marca Perkin-Elmer©. El espectrómetro se completa con una esfera integradora de la marca PIKE©.
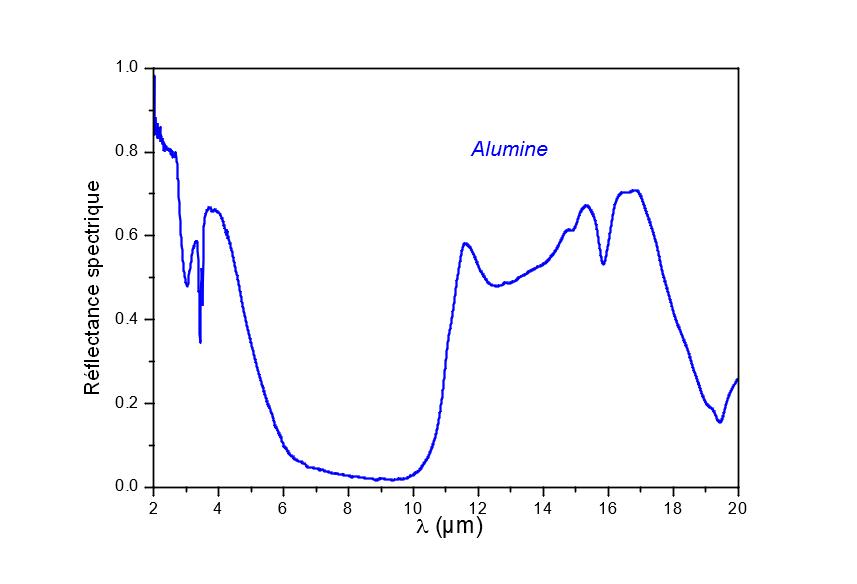
Figura 3
Factor de reflexión espectral en función de la longitud de onda de una muestra de alúmina.
Estos dispositivos experimentales se pueden ver en la figura 2. A pesar de esta limitación, la medición espectral proporciona información exacta sobre las variaciones de la emisividad en función de la temperatura. Combinando las dos técnicas (medición espectral y medición de banda ancha) podemos volver a una medición exacta de la emisividad. Podemos ilustrar este método estudiando la alúmina (Al2O3):
Por ejemplo, en el caso de la alúmina, la muestra utilizada es de cerámica amorfa. Este tipo de material es un caso de libro porque su emisividad espectral direccional varía mucho en torno a los 10 µm (figura 3), es decir, en torno a la emisión máxima de un cuerpo a temperatura ambiente.
Esto ocurre con frecuencia en este tipo de cerámica. Además, no se pueden utilizar datos bibliográficos. De hecho, dependiendo de la variedad alotrópica, el grado de cristalización, los diferentes tratamientos térmicos, etc., los valores de la emisividad espectral direccional de la alúmina son muy variables [6].
Cuando la temperatura de la superficie estudiada varía desde la temperatura ambiente hasta temperaturas más altas, la luminancia máxima de la función de Planck L ( λ, T) se desplaza 10 µm hacia longitudes de onda más cortas. La luminancia máxima se alcanza para una longitud de onda λmax(en µm) = 3000 /T, con T en K.
En el caso de la alúmina, esto tiene el efecto de aumentar la tensión en una región espectral mucho más emisiva. Por lo tanto, la emisividad aumenta con la temperatura. Podemos calcular la emisividad teniendo en cuenta únicamente la banda espectral de 1 a 20 µm. Estos datos se presentan en la tabla 1. Este cálculo descuida una parte importante del espectro útil. Por lo tanto, el valor de emisividad calculado es incorrecto.
Sin embargo, dada la monotonía de la función de Planck para longitudes de onda superiores a 20 µm para esta temperatura, las variaciones de la emisividad en función de la temperatura solo dependen, por lo tanto, de la banda espectral de 1 a 20 µm. Al no conocer el valor de la emisividad, podemos deducir con bastante precisión el coeficiente de variación de la emisividad en función de la temperatura. Si podemos medir por otros medios la emisividad para una temperatura superior a la temperatura ambiente, podemos deducir la emisividad a todas las temperaturas en torno a los 300 K.
Esto se puede observar en los gráficos de la figura 4. A partir de las mediciones espectrales (gráfico superior de la figura 4) podemos obtener las variaciones de la emisividad en función de la temperatura (gráfico inferior de la figura 4, línea azul). El emisímetro EM2 de CERTES [2] (figura 5) permite obtener un valor no sesgado de la emisividad, pero solo a 360 K. A partir de estos dos datos, volvemos a la emisividad no sesgada en función de la temperatura (gráfico inferior de la figura 4, línea roja).
Figura 4.
Reflectancia espectral de la alúmina, arriba; cálculo de la emisividad a partir de mediciones espectrales y un emisímetro de banda ancha (EM2 [2]), abajo.
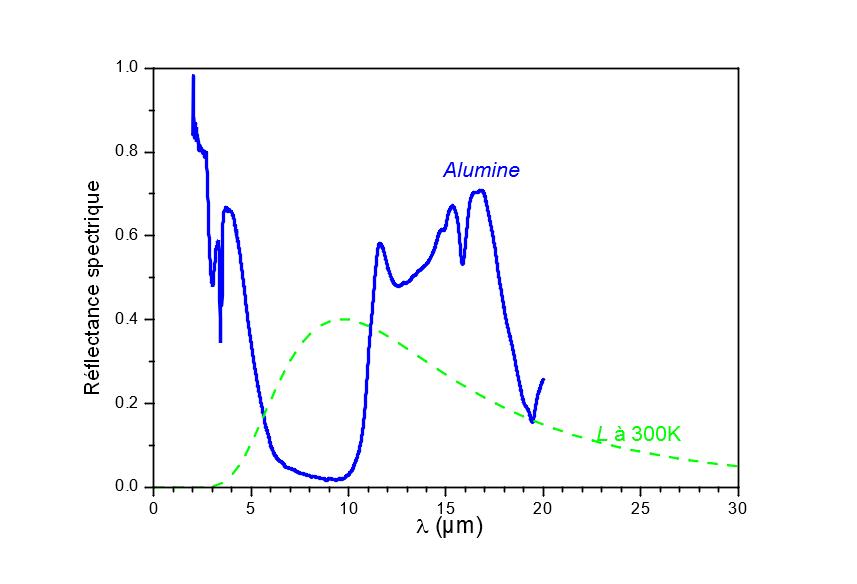
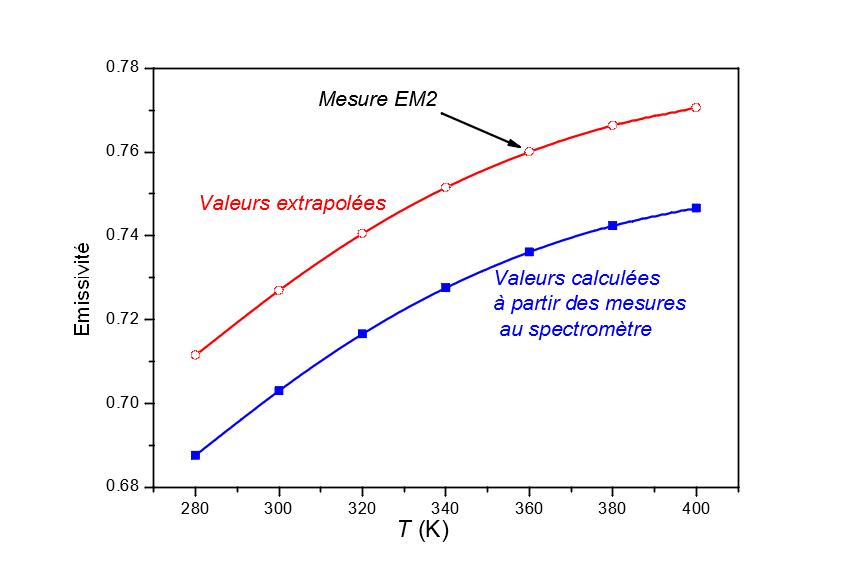

Figura 5
Emisímetro EM2, desarrollado en CERTES Breveté en 2012 (FR 2987121)
Conclusión
La medición de las propiedades espectrales de las superficies en el dominio infrarrojo es esencial para conocer el comportamiento radiativo de estas superficies. La única medición de la emisividad con un aparato comercial no permite alcanzar un valor exacto de la emisividad. La mayoría de estos dispositivos comerciales se diseñaron para el control de la producción, no para obtener un valor de emisividad direccional.
La combinación de los dos métodos de medición y un buen conocimiento de las características de los dispositivos utilizados permiten obtener mediciones libres de errores sistemáticos.
La numeración no corresponde al orden de aparición en el documento.
- Principio y aplicaciones, Meas. Sci. Technology.17, 2950 (2006)
- J-P. Monchau, M. Marchetti, L. Ibos, J. Dumoulin, V. Feuillet, Y. Candau, Mediciones de emisividad infrarroja de materiales de construcción e ingeniería civil: un nuevo dispositivo para medir la emisividad, Int. J. Thermophys., en prensa
- J. Hameury, B. Hay, J. R. Filtz, Medición de la emisividad hemisférica total mediante una técnica calorimétrica,
Int. J. Thermophys, 28, 1607 (2007) - O. Rozenbaum, D. De Sousa Meneses, Y. Auger, S. Chermanne y P. Echegut, Método espectroscópico para
medir la emisividad espectral de materiales semitransparentes a altas temperaturas, Rev. Sci. Instrum. 70, 4020 (1999) - K.E. Nelson, E.E.Leudke, J.T.Bevans, Un dispositivo para la medición rápida de la emisividad total, Journal of
Spacecraft and Rockets, 3, 758 (1966) - Propiedades termofísicas de los materiales sólidos a alta temperatura, vol. 4, Y. S. Touloukian, editor
CUADRO
Errores debidos a la modulación de la temperatura de la fuente.
Este caso se refiere a los métodos que utilizan un método reflectométrico con una fuente modulada. Se supone que la distribución espectral de la fuente no varía significativamente cuando las variaciones de temperatura son pequeñas. Esta suposición es exacta, sin embargo, con estos métodos no se mide el flujo reflejado por la muestra, sino solo las variaciones del flujo reflejado.
Esto también se aplica a las fuentes cortadas por una pantalla móvil (chopper). De hecho, en este caso, se mide la alternancia entre la temperatura de la fuente y la de la pantalla. Si la temperatura T es una función periódica del tiempo, debemos considerar su expresión como una función del tiempo T(t), donde t es el tiempo. La señal medida por el detector es igual a:
![]()
donde L(λ,T) es la luminancia del cuerpo negro para la longitud de onda λ y la temperatura T. Esta diferencia se ilustra en la figura 6.
Dado que en este caso solo nos interesan las variaciones periódicas de esta luminancia, la medición es, por lo tanto, proporcional a la amplitud pico a pico denotada A medida por el detector para variaciones de temperatura ΔT por encima de la temperatura mínima (por razones de simplicidad en la redacción, se supone que la temperatura varía entre T y T+ΔT) :
Si medimos la señal correspondiente al flujo incidente, podemos obtener el coeficiente de reflexión total en la cobertura espectral de la banda por el detector :
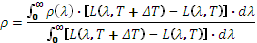
Por lo tanto, se puede observar que, en realidad, la reflectancia se mide con una fuente que tiene una distribución espectral igual a la diferencia de luminancia de dos fuentes de diferentes temperaturas. Esta distribución espectral difiere significativamente de la distribución espectral de un cuerpo negro a temperatura media.
La figura 7 muestra la luminancia de un cuerpo negro a 300 K y 360 K, así como la diferencia de luminancia entre dos cuerpos negros a 300 K y 305 K. Las curvas se han normalizado para facilitar la lectura. Obsérvese que la distribución espectral de la fuente modulada ya no sigue la ley de Planck, sino que se aproxima a la distribución espectral de un cuerpo negro a 360 K. Para que este error tenga una influencia insignificante, la muestra debe poder asimilarse a un cuerpo gris de alrededor de 10 µm o conocer las propiedades espectrales de la superficie estudiada.
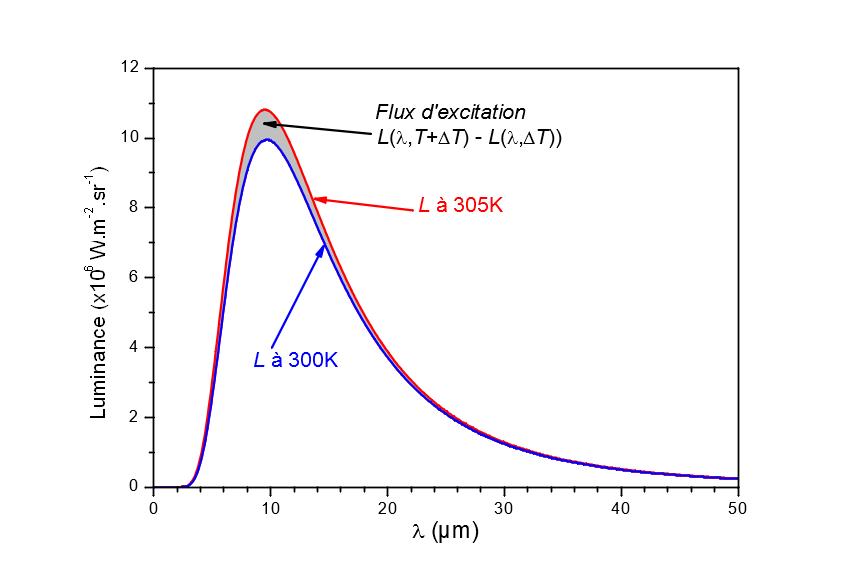
Figura 6
Determinación de la distribución espectral del flujo de excitación de una fuente modulada
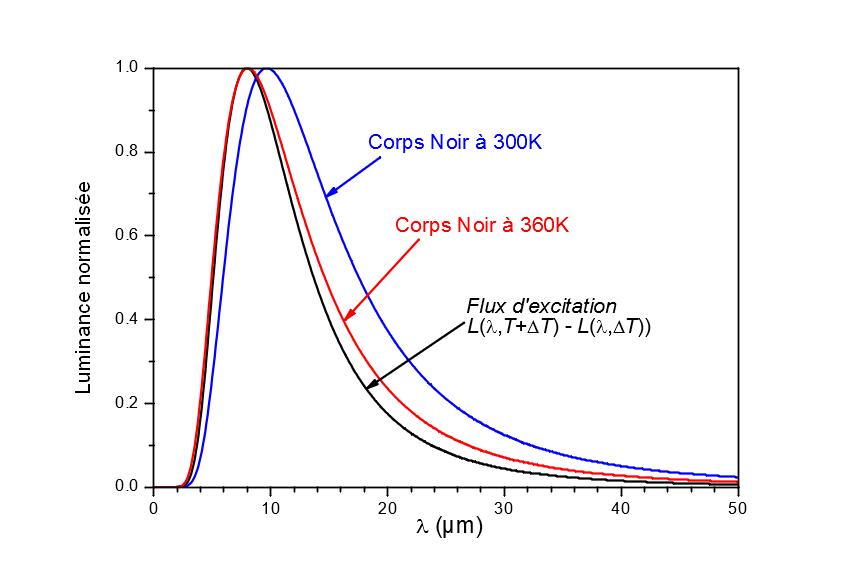
Figura 7.
Comparación de la distribución espectral del flujo de excitación de una fuente modulada alrededor de 300 K con la de un cuerpo negro a 360 K.
Nuestro equipo le asesora para satisfacer mejor sus expectativas.


