Importance and limitation of spectral measurements
Importanza e limiti delle misurazioni spettrali per la misurazione dell’emissività
Autori:
Jean-Pierre MONCHAU, THEMACS Ingénierie, 2bis rue Alfred Nobel, 77420 Champs sur Marne,monchau@themacs.fr
Laurent IBOS, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, ibos@u-pec.fr
Mario MARCHETTI, CEREMA, Laboratoire Régional de Nancy,71, rue de la Grande Haie – 54510 Tomblaine,Mario. Marchetti@cerema.fr
Jean DUMOULIN, IFSTTAR, Dépt. CoSys, Route de Bouaye, 44344 Bouguenais Cedex, jean.dumoulin@ifsttar.fr
Vincent FEUILLET, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, vincent.feuillet@u-pec.fr
Emissività
L’emissività è una proprietà termofisica dei materiali importante per quantificare lo scambio termico per irraggiamento. È anche essenziale per misurare la temperatura superficiale da una misurazione della luminanza, come ad esempio mediante termografia a infrarossi.
Quest’ultima tecnica sta diventando sempre più diffusa con la democratizzazione delle termocamere con array di microbolometri. La misurazione dell’emissività a temperatura ambiente viene generalmente effettuata con il metodo indiretto utilizzando la legge di Kirchhoff che mette in relazione l’emissività con la riflettanza per un materiale opaco. Esistono diversi dispositivi commerciali, tuttavia questi dispositivi presentano errori di misurazione. Per correggere questi difetti, è necessario conoscere il comportamento spettrale del materiale.
La misurazione del fattore di riflessione spettrale con uno spettrometro infrarosso a trasformata di Fourier (FTIR) dotato di una sfera integratrice consente di ottenere queste informazioni. La limitazione spettrale delle sfere integratrici (generalmente 1-20 µm), tuttavia, rende necessario l’uso di un emissimetro che copra una gamma spettrale più ampia.
CERTES ha sviluppato un protocollo di misurazione che combina le due tecniche (a banda larga e spettrale) per ottenere un valore di emissività non distorto, corretto per le variazioni di temperatura della sorgente. Questo metodo è stato testato con successo su diversi materiali, in particolare ceramiche come l’allumina (Al2O3) che presentano forti variazioni di riflettanza nella banda da 1 a 20 µm. Questi risultati sono presentati in questo articolo.
Definizione di emissività
Max Planck ha determinato teoricamente l’emissività spettrale di un corpo ideale chiamato corpo nero utilizzando la teoria quantistica (Figura 1). Le superfici reali irradiano in modo simile, ma l’emissività è ponderata da un coefficiente adimensionale chiamato emissività.
Questo coefficiente dipende dal materiale, dalla sua temperatura, dalla lunghezza d’onda e dall’incidenza (in questo caso l’angolo di emissione). Gli ingegneri termici preferiscono utilizzare un coefficiente integrato su tutto lo spettro e per tutte le incidenze chiamato emissività emisferica totale per poter, ad esempio, quantificare la quantità di calore perso per irraggiamento da una superficie.
La difficoltà consiste quindi nel determinare questo coefficiente senza trascurare le lunghezze d’onda o le incidenze.
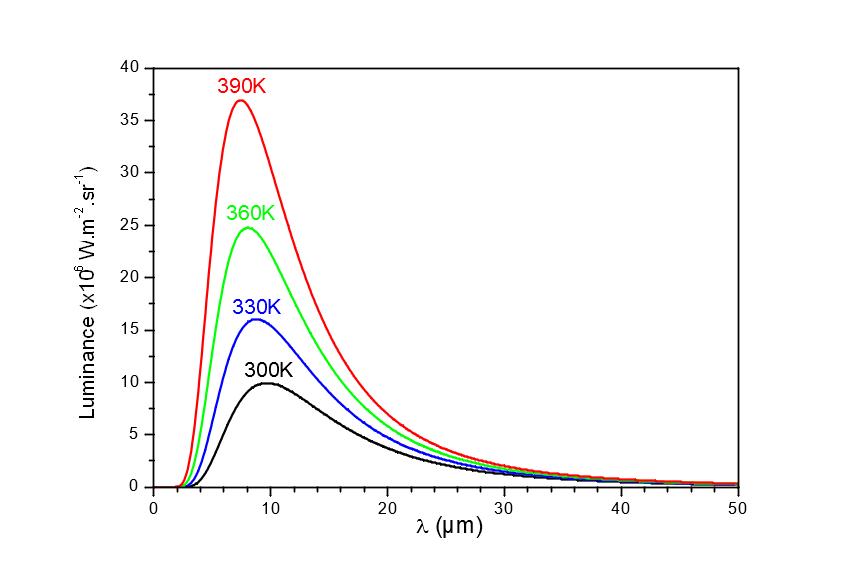
Figura 1
Luminanza di un corpo nero L(λ) per diverse temperature T
Per misurare l’emissività esistono diversi approcci che possiamo classificare in due categorie: i metodi diretti misurano la radiazione energetica della superficie studiata, mentre i metodi indiretti deducono l’emissività da altre proprietà ottiche della superficie.
Tra i metodi diretti si può citare il metodo calorimetrico, che consiste nel misurare la potenza elettrica da fornire a un campione (collocato in un criostato sotto vuoto) per mantenere la sua temperatura superficiale uguale alla temperatura alla quale si desidera conoscere l’emissività. Il Laboratorio Nazionale di Metrologia e Prova (LNE) dispone di un banco di misura di questo tipo [3].
Un altro metodo, detto radiometrico, consiste nel misurare la radiazione termica proveniente dalla superficie del materiale. Questa misurazione può essere effettuata in funzione dell’angolo per ottenere l’emissività direzionale e in funzione della lunghezza d’onda (ad esempio con uno spettrometro FTIR) per ottenere l’emissività spettrale direzionale. Il dispositivo CEMHTI (Extreme Conditions and High Temperature Materials and Irradiation) consente questo tipo di misurazione a temperature molto elevate [4].
Per la misurazione dell’emissività a temperatura ambiente, il livello del flusso è troppo basso per essere misurato con buona precisione: questo è il campo privilegiato dei metodi indiretti. Questi utilizzano la legge di Kirchhoff che mette in relazione l’emissività ε con la riflettanza ρ e la trasmittanza τ per una data lunghezza d’onda λ :
![]()
l’emissività è uguale all’assorbimento. Per un materiale opaco, l’emissività è quindi pari a:
![]()
Per ottenere l’emissività totale dobbiamo quindi aggiungere il fattore di riflessione spettrale (è la prima volta che vedo questa parola) ponderato dalla distribuzione spettrale dell’energia del corpo nero alla temperatura alla quale si desidera conoscere l’emissività :
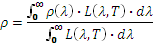
L’altra soluzione consiste nel misurare il fattore di riflessione globale illuminando la superficie con una sorgente luminosa che abbia questa distribuzione di energia.
Diversi dispositivi commerciali che misurano l’emissività utilizzano questo metodo. La loro principale qualità è quella di misurare la riflettanza in una banda spettrale compresa tra 1 e 50 µm, che rappresenta il 95% dell’energia irradiata da un corpo nero a temperatura ambiente (circa 300 K). Tuttavia, integrano il fattore di riflessione per una distribuzione spettrale diversa dalla temperatura ambiente.
Infatti, utilizzano corpi neri o grigi come sorgenti di infrarossi a una temperatura superiore alla temperatura ambiente. Queste sorgenti hanno distribuzioni spettrali diverse da quelle di un corpo nero a 300 K. Questa differenza nella distribuzione spettrale porta a errori di misurazione dell’emissività per corpi non grigi fino al 5%. Questo difetto non è una novità.
Infatti, lo standard ASTM E408-71 (Metodo di prova standard per l’emissività normale totale di una superficie utilizzando tecniche di misurazione con ispettori) lo afferma. Possiamo anche fare riferimento a [5], dove questo tipo di errore è brevemente menzionato.
Gli emissimetri sviluppati presso il CERTES [1,2] utilizzano sorgenti infrarosse modulate in temperatura a temperature molto vicine alla temperatura ambiente. Il problema rimane irrisolto perché la modulazione influisce in modo significativo sulla distribuzione spettrale della sorgente (vedi riquadro 1).
Per eliminare questa incertezza, è necessario misurare la riflettanza spettrale direzionale emisferica (che è uguale alla riflettanza emisferica direzionale per ragioni di reciprocità). Gli unici dispositivi commerciali che consentono di effettuare questa misurazione sono le sfere integratrici. Possono essere accoppiate a spettrometri FTIR e consentono misurazioni nella banda spettrale 1-20 µm.
Ciò che oggi limita la gamma spettrale delle sfere integratrici commerciali è il rivestimento interno di queste ultime. Esso deve essere perfettamente diffusivo (comportamento lambertiano). Ciò non è più vero per lunghezze d’onda superiori a 20 µm. Dobbiamo quindi accontentarci di questa banda spettrale che rappresenta solo il 76% dell’energia irradiata a 300 K. Il dispositivo utilizzato dal CERTES e dalla THEMACS Engineering è uno spettrometro a infrarossi con trasformata di Fourier FRONTIER© della marca Perkin-Elmer©. Lo spettrometro è completato da una sfera integratrice della marca PIKE©.
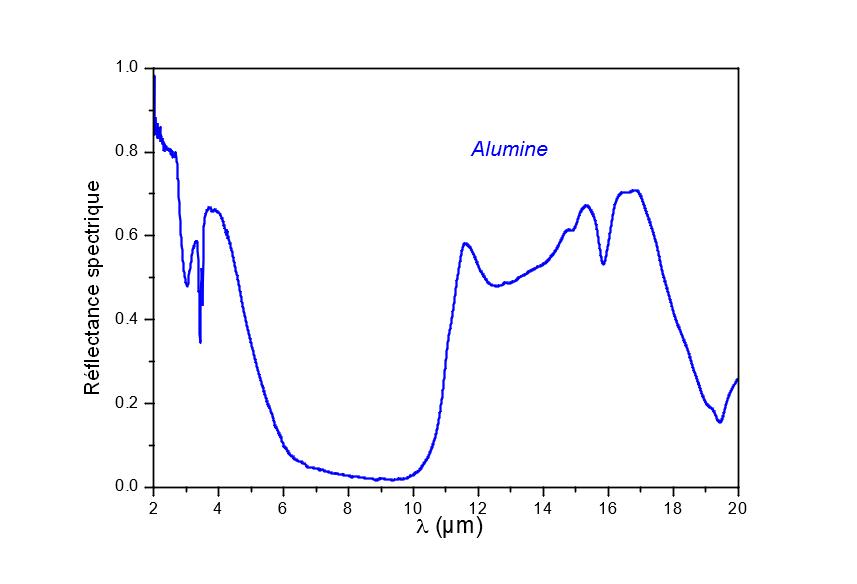
Figura 3
Fattore di riflessione spettrale in funzione della lunghezza d’onda di un campione di allumina
Questi dispositivi sperimentali sono visibili nella figura 2. Nonostante questa limitazione, la misurazione spettrale fornisce informazioni precise sulle variazioni dell’emissività in funzione della temperatura. Combinando le due tecniche (misurazione spettrale e misurazione a banda larga) è possibile ottenere una misurazione esatta dell’emissività. È possibile illustrare questo metodo studiando l’allumina (Al2O3):
Ad esempio, nel caso dell’allumina, il campione utilizzato è sotto forma di ceramica amorfa. Questo tipo di materiale è un caso da manuale perché la sua emissività spettrale direzionale varia notevolmente intorno ai 10 µm (Figura 3), cioè intorno all’emissione massima di un corpo a temperatura ambiente.
Questo è spesso il caso per questo tipo di ceramica. Inoltre, i dati bibliografici non possono essere utilizzati. Infatti, a seconda della varietà allotropica, del grado di cristallizzazione, dei diversi trattamenti termici, ecc., i valori dell’emissività spettrale direzionale dell’allumina sono molto variabili [6].
Quando la temperatura della superficie studiata varia dalla temperatura ambiente a temperature più elevate, la luminanza massima della funzione di Planck L ( λ, T) si sposta di 10 µm verso lunghezze d’onda più corte. La luminanza massima viene raggiunta per una lunghezza d’onda λmax(in µm) = 3000 /T, con T in K.
Per l’allumina, ciò ha l’effetto di aumentare lo stress su una regione spettrale molto più emissiva. L’emissività aumenta quindi con la temperatura. È possibile calcolare l’emissività tenendo conto solo della banda spettrale da 1 a 20 µm. Questi dati sono presentati nella tabella 1. Questo calcolo trascura una parte importante dello spettro utile. Il valore di emissività calcolato è quindi errato.
Tuttavia, data la monotonicità della funzione di Planck per lunghezze d’onda superiori a 20 µm per questa temperatura, le variazioni dell’emissività in funzione della temperatura dipendono quindi solo dalla banda spettrale compresa tra 1 e 20 µm. Non conoscendo il valore dell’emissività, possiamo quindi dedurre con una certa precisione il coefficiente di variazione dell’emissività in funzione della temperatura. Se siamo in grado, con altri mezzi, di misurare l’emissività per una temperatura superiore alla temperatura ambiente, possiamo quindi dedurre l’emissività a tutte le temperature intorno ai 300 K.
Ciò è visibile nei grafici della figura 4. Dalle misurazioni spettrali (grafico superiore della figura 4) possiamo ottenere le variazioni dell’emissività in funzione della temperatura (grafico inferiore della figura 4, linea blu). L’emissimetro EM2 di CERTES [2] (figura 5) consente di ottenere un valore non distorto dell’emissività, ma solo a 360 K. Da queste due informazioni, torniamo all’emissività non distorta in funzione della temperatura (grafico inferiore della figura 4, linea rossa).
Tabella 1
Emissività calcolata dai dati spettrali tra 1 e 20 µm a diverse temperature
Figura 4
Riflettanza spettrale dell’allumina, in alto; calcolo dell’emissività da misurazioni spettrali e un emissimetro a banda larga (EM2 [2]), in basso.
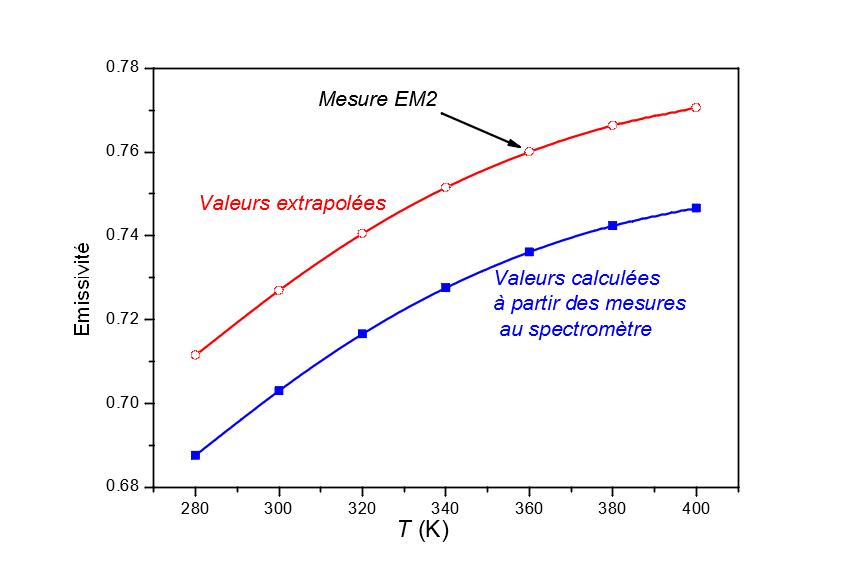

Figura 5
Emissimetro EM2, sviluppato da CERTES Breveté nel 2012 (FR 2987121)
Conclusione
La misurazione delle proprietà spettrali delle superfici nel dominio dell’infrarosso è essenziale per conoscere il comportamento radiativo di tali superfici. La sola misurazione dell’emissività con un apparecchio commerciale non consente di ottenere un valore esatto dell’emissività. La maggior parte di questi dispositivi commerciali è stata progettata per il controllo della produzione, non per ottenere un valore di emissività direzionale.
La combinazione dei due metodi di misurazione e una buona conoscenza delle caratteristiche dei dispositivi utilizzati consentono di ottenere misurazioni prive di errori sistematici.
La numerazione non corrisponde all’ordine di apparizione nel documento.
- L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau, Dispositivo di misurazione dell’emissività infrarossa:
Principi e applicazioni, Meas. Sci. Technology.17, 2950 (2006) - J-P. Monchau, M. Marchetti, L. Ibos, J. Dumoulin, V. Feuillet, Y. Candau, Misurazioni dell’emissività infrarossa di materiali da costruzione e di ingegneria civile: un nuovo dispositivo per la misurazione dell’emissività, Int. J. Thermophys., in stampa
- J. Hameury, B. Hay, J. R. Filtz, Misurazione dell’emissività emisferica totale utilizzando una tecnica calorimetrica,
Int. J. Thermophys, 28, 1607 (2007) - O. Rozenbaum, D. De Sousa Meneses, Y. Auger, S. Chermanne e P. Echegut, Un metodo spettroscopico per
misurare l’emissività spettrale di materiali semitrasparenti fino ad alte temperature, Rev. Sci. Instrum. 70, 4020 (1999) - K.E. Nelson, E.E.Leudke, J.T.Bevans, Un dispositivo per la misurazione rapida dell’emissività totale, Journal of
Spacecraft and Rockets, 3, 758 (1966) - Proprietà termofisiche dei materiali solidi ad alta temperatura, Vol. 4, Y. S. Touloukian Editore
SCATOLA
Errori dovuti alla modulazione della temperatura della sorgente
Questo caso riguarda i metodi che utilizzano un metodo riflettometrico che coinvolge una sorgente modulata. Si presume che la distribuzione spettrale della sorgente non vari in modo significativo quando le variazioni di temperatura sono minime. Questa ipotesi è esatta, tuttavia con questi metodi non si misura il flusso riflesso dal campione, ma solo le variazioni del flusso riflesso.
Ciò vale anche per le sorgenti interrotte da uno schermo mobile (chopper). Infatti, in questo caso, viene misurata l’alternanza tra la temperatura della sorgente e quella dello schermo. Se la temperatura T è una funzione periodica del tempo, dobbiamo considerare la sua espressione come funzione del tempo T(t) dove t è il tempo. Il segnale misurato dal rilevatore è pari a :
![]()
dove L(λ,T) è la luminanza del corpo nero per la lunghezza d’onda λ e la temperatura T. Questa differenza è illustrata nella Figura 6.
Poiché in questo caso ci interessano solo le variazioni periodiche di questa luminanza, la misurazione è quindi proporzionale all’ampiezza picco-picco indicata con A misurata dal rilevatore per variazioni di temperatura ΔT superiori alla temperatura minima (per semplicità di scrittura, si ipotizza che la temperatura vari tra T e T+ΔT) :
Se misuriamo il segnale corrispondente al flusso incidente, possiamo ottenere il coefficiente di riflessione totale nella copertura spettrale della banda dal rilevatore :
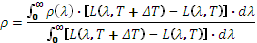
Si può quindi vedere che, in realtà, la riflettanza viene misurata con una sorgente avente una distribuzione spettrale pari alla differenza di luminanza di due sorgenti di temperature diverse. Questa distribuzione spettrale differisce in modo significativo dalla distribuzione spettrale di un corpo nero a temperatura media.
La figura 7 mostra la luminanza di un corpo nero a 300 K e 360 K, nonché la differenza di luminanza tra due corpi neri a 300 K e 305 K. Le curve sono state normalizzate per facilitare la lettura. Si noti che la distribuzione spettrale della sorgente modulata non segue più la legge di Planck, ma si avvicina alla distribuzione spettrale di un corpo nero a 360 K. Affinché questo errore abbia un’influenza trascurabile, il campione deve poter essere assimilato a un corpo grigio intorno ai 10 µm o conoscere le proprietà spettrali della superficie studiata.
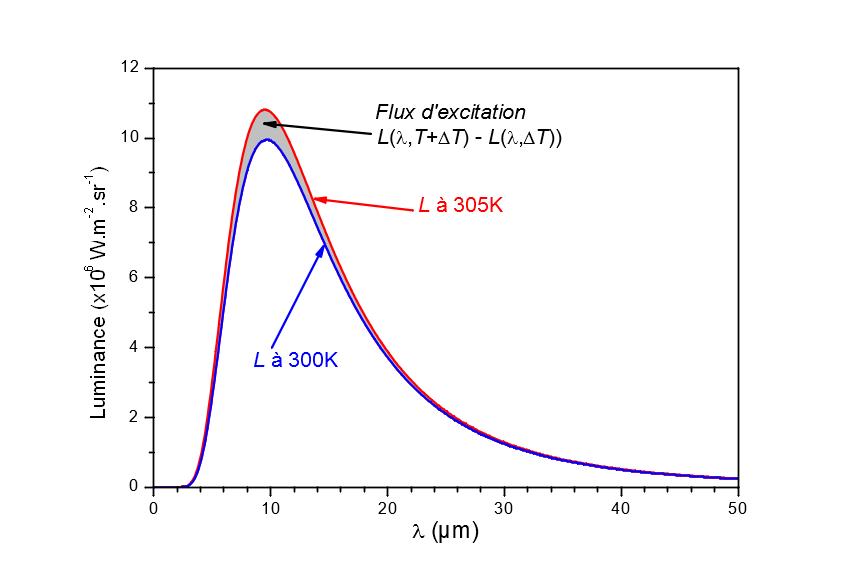
Figura 6
Determinazione della distribuzione spettrale del flusso di eccitazione di una sorgente modulata
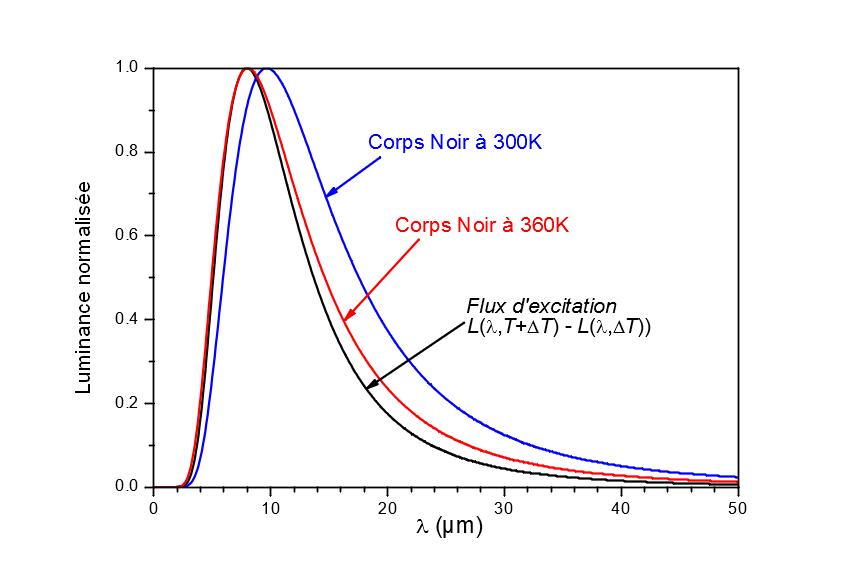
Figura 7
Confronto tra la distribuzione spettrale del flusso di eccitazione di una sorgente modulata intorno a 300 K e quella di un corpo nero a 360 K.
Il nostro team vi consiglia per soddisfare al meglio le vostre aspettative

