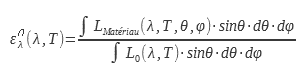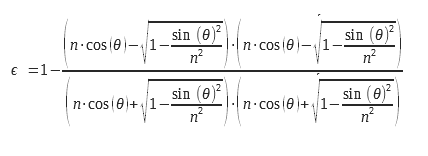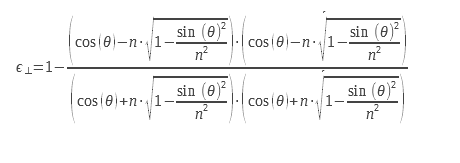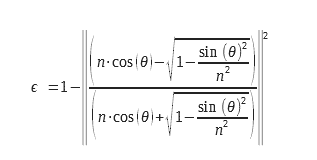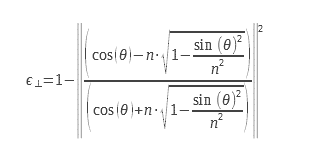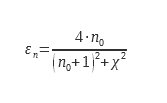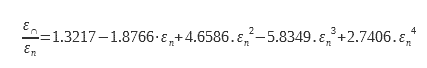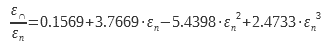Mesure de l’émissivité thermique
Mesure de l’émissivité thermique
1. Définitions des différentes émissivités
Les surfaces des matériaux peuvent échanger de l’énergie sous forme de rayonnement. La quantité d’énergie que peut émettre une surface dépend de sa température et de sa nature. La loi de Planck précise la luminance énergétique spectrale pour une surface théorique appelée corps noir :
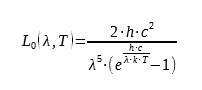
où h = 6.62617.10−34 J.s est la constante de Planck, c la vitesse de la lumière dans le milieu considéré (on prendra la valeur de c dans le vide : c = 299792458m.s−1) et k = 1.38066.10−23 J.K−1 la constante de Boltzmann. La luminance énergétique spectrale L0 s’exprime en W.m-3.sr-1.
Pour un matériau donné, cette luminance est pondérée par un coefficient compris entre 0 et 1 et appelé émissivité. On la note ε.
Ce coefficient peut dépendre de la longueur d’onde, de l’incidence et de la température :
On classe les émissivités selon les domaines spatial et spectral du rayonnement. On appelle émissivité totale l’émissivité calculée sur l’ensemble du spectre et émissivité monochromatique l’émissivité calculée pour une seule longueur d’onde. On appelle émissivité hémisphérique l’émissivité calculée pour l’ensemble des directions et émissivité directionnelle celle calculée suivant une seule direction.
1.1 Emissivité monochromatique directionnelle
L’émissivité monochromatique directionnelle notée est le rapport entre la luminance du matériau et celle du corps noir pour une direction et une longueur d’onde données. C’est la grandeur qui permet la description la plus fine pour un matériau donné :
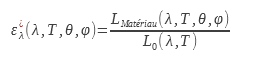
L0 ne dépend pas de l’incidence pour un corps noir.
La plupart des matériaux ont une émissivité ne dépendant pas de l’orientation et ne dépend donc pas de ϕ.
Pour les surfaces lisses cette émissivité peut dépendre de la polarisation de la lumière.
1.3 Emissivité totale directionnelle
L’émissivité totale directionnelle est le rapport entre la luminance rayonné par la surface du matériau étudié par la luminance rayonné par le corps noir sur l’ensemble du spectre électromagnétique:
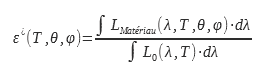
Cette valeur de l’émissivité intéresse les utilisateurs de caméras thermiques. En effet, elle permet de relier la luminance dans une direction avec la température. Ce calcul ou cette mesure d’émissivité peut se faire dans une bande de longueur d’onde identique à celle de la caméra ou dans une bande spectrale donnée :
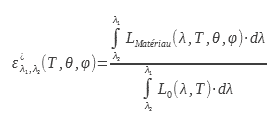
1.4 Emissivité totale hémisphérique
L’émissivité totale hémisphérique notée ε est le rapport entre l’émittance totale hémisphérique du matériau par celle du corps noir pour l’ensemble des longueurs d’ondes à une température donnée:
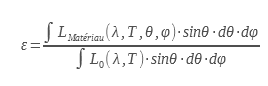
C’est cette émissivité qui intéresse les thermiciens pour effectuer des bilans thermiques de parois opaques. Elle permet de calculer les échanges radiatifs d’une surface portée à la température T.
1.5 Cas particuliers
Si l’émissivité d’un matériau ne dépend pas de la longueur d’onde, on qualifie celui-ci de corps gris. Cette propriété ne se rencontre pas dans la réalité et on qualifiera de corps gris, un corps pour lequel l’émissivité ne varie pas dans le domaine spectral étudié. Un corps gris dont les propriétés spectrales ne varient pas en fonction de la température possède une émissivité ne variant pas non plus en fonction de la température. A l’inverse une surface ayant une émissivité spectrale variant avec la longueur d’onde aura une émissivité totale variant avec la température, du fait que le spectre de rayonnement du corps noir varie avec la température.
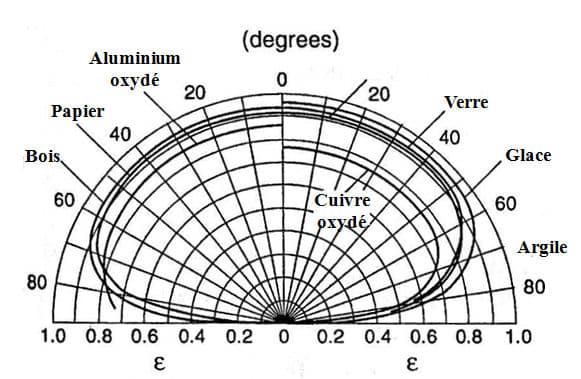
Comme nous venons de le voir, l’émissivité d’un matériau réel dépend généralement aussi de l’angle d’émission. Ce n’est donc pas une surface lambertienne. Pour les diélectriques cependant, l’émissivité varie peu dans une large plage angulaire (de 0 à 60◦). Dans ce domaine angulaire, ils sont considérés comme lambertiens. La figure 1 d’après Maldague représente l’émissivité totale directionnelle en fonction de l’angle pour un certain nombre de matériaux. On peut constater que celle-ci ne varie pas jusqu’à un angle de 60◦. En outre, la loi de variation de l’émissivité en fonction de l’angle montre une similitude de forme.
2. Calcul de l’émissivité à partir de l’indice complexe
La loi de conservation de l’énergie se traduit dans le cas du rayonnement électromagnétique par la loi de Kirchhoff. Dans le cas général, cette loi relie pour une longueur d’onde donnée le facteur de transmission, le facteur de réflexion directionnel hémisphérique à l’absorption qui est dans ce cas égal à l’émissivité :
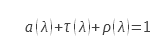
Où a est le facteur d’absorption spectral, τ le facteur de transmission spectral et ρ le facteur de réflexion directionnel hémisphérique.
Pour un matériau opaque cette relation devient :
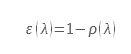
Puisque ε=a et que pour un matériau opaque τ=0.
L’équation (8) est à la base de toutes les méthodes indirectes de mesure de l’émissivité. Elle permet en outre de calculer l’émissivité à partir du facteur de réflexion lui-même calculé par les relations de Fresnel. Cette approche n’est valable que pour les dioptres, c’est-à-dire pour les surfaces lisses.
2.1 Calcul de l’émissivité pour les deux polarisations de la lumière
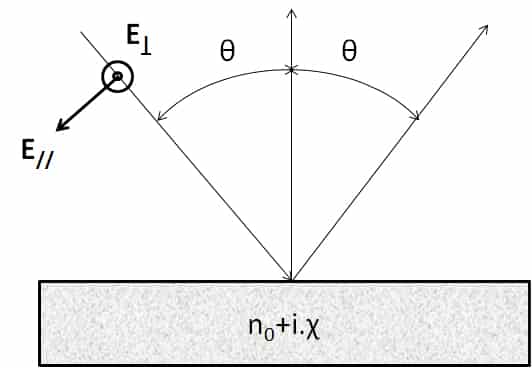
Pour le dioptre plan, on peut calculer l’émissivité à partir de l’expression des coefficients de réflexion, calculés à partir de l’indice complexe, n = n0+i.χ. On peut retrouver ce calcul détaillé dans Kauder à partir des équations de Maxwell. Ces expressions sont déduites des coefficients de Fresnel pour la réflexion, on peut les trouver dans Lorrain et Corson. Les équations 9 et 10 peuvent être utilisées avec les indices complexes ce qui permet de les utiliser pour le calcul de l’émissivité des métaux. Des considérations de conditions aux limites au niveau du dioptre imposent de calculer un coefficient de réflexion et donc d’émissivité pour deux polarisations distinctes. Ces polarisations sont explicitées sur le schéma de la Figure 2.
Pour une lumière non polarisée, on doit effectuer la moyenne arithmétique des deux émissivités correspondant aux deux polarisations. Les expressions des deux émissivités pour les deux polarisations sont présentés ci-dessous :
On peut les écrire sous une autre forme :
2.2 Cas des diélectriques
La Figure 3 issue de Kauder montre l’émissivité directionnelle en fonction de l’angle pour un diélectrique ayant un indice de réfraction de 1.5 : cela correspond à une permittivité diélectrique relative de 2.25 :
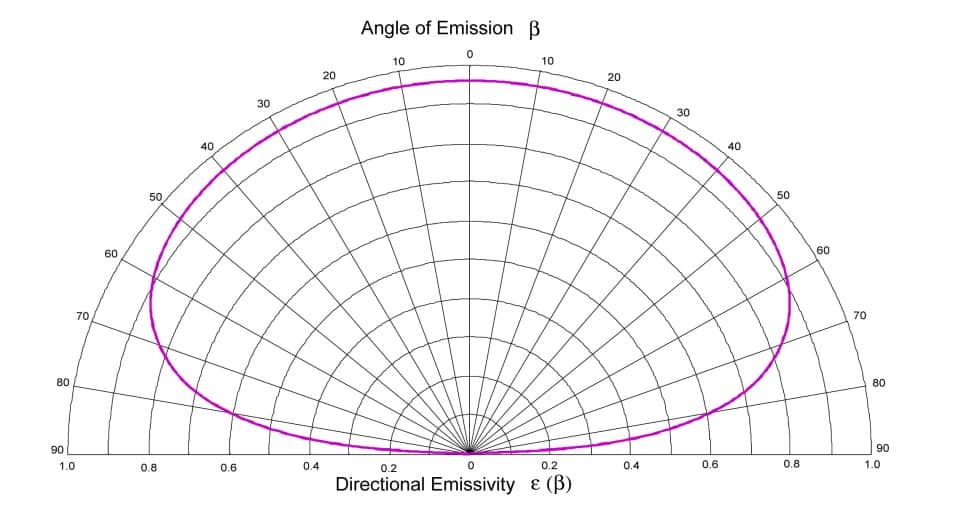
Figure 3
Emissivité directionnelle en fonction de l’angle pour un diélectrique d’indice de réfraction de 1.5 Kauder
Ce sont typiquement les caractéristiques d’un verre à base de boro-silicates. On constate que l’on retrouve la même forme d’indicatrice d’émissivité par la théorie que celles mesurées expérimentalement (Figure 1). Puisque le seul paramètre pouvant faire varier l’émissivité d’un dioptre diélectrique lisse est l’indice de réfraction réel, pour un indice de réfraction donné, on aura toujours la même indicatrice d’émissivité. De ce fait, on peut calculer par intégration sur l’ensemble de l’hémisphère l’émissivité hémisphérique.
Le rapport entre l’émissivité hémisphérique et l’émissivité directionnelle normale n’est donc fonction que de l’indice de réfraction, et donc seulement de l’émissivité directionnelle normale (Figure 1). On pourra donc déduire l’émissivité hémisphérique de l’émissivité directionnelle normale, et inversement. Ces rapports sont tabulés dans la norme NF EN 12898 concernant la détermination de l’émissivité pour le verre de construction. Cette étude peut être utilisée pour un diélectrique non lisse avec une bonne approximation. En effet, le caractère rugueux n’affecte que très peu l’indicatrice d’émissivité d’un diélectrique. Ces considérations seront reprise dans la partie 1.9.
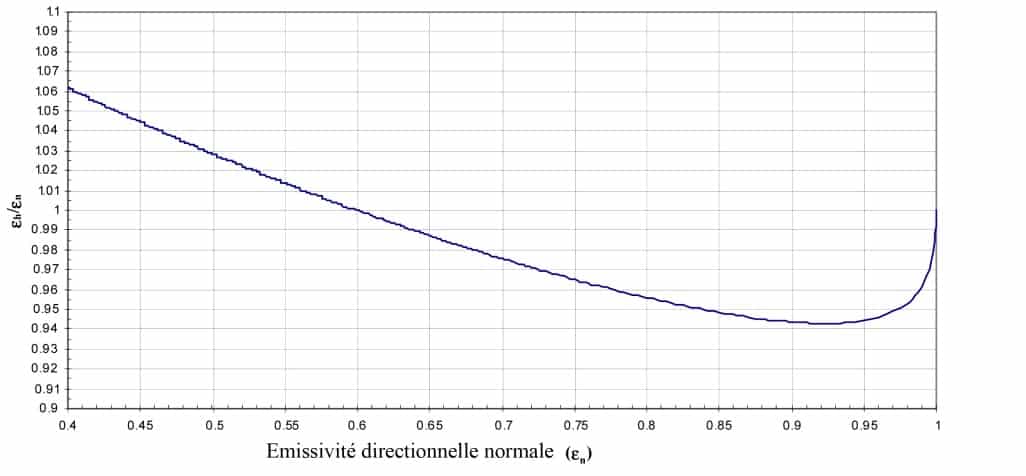
Figure 4
Rapport entre l’émissivité hémisphérique et l’émissivité directionnelle normale en fonction de l’émissivité directionnelle normale pour les diélectriques lisses Kauder
2.3 Cas des métaux et conducteurs
De la même manière, on peut tracer l’indicatrice d’émissivité pour un dioptre air/métal. On obtient une indicatrice d’émissivité théorique similaire à ce que l’on peut obtenir sur un métal comme l’aluminium. Celle représentée Figure 5 issue de Kauder est calculée pour un indice de réfraction typique d’un métal tel que l’aluminium : n = 5.7 + 9.7i. La correspondance entre l’émissivité hémisphérique et l’émissivité directionnelle normale existe aussi pour les conducteurs, cependant l’indicatrice d’émissivité est différente. Il faut donc traiter les conducteurs séparément des diélectriques pour déterminer le rapport entre les deux émissivités. Cette étude ne peut être utilisée pour un conducteur non lisse. En effet le caractère rugueux affecte fortement l’indicatrice d’émissivité d’un métal car l’émissivité d’un métal varie beaucoup avec la rugosité de celui-ci. On se réfèrera à [30] pour une étude plus détaillée de l’émissivité des métaux en fonction de la rugosité.
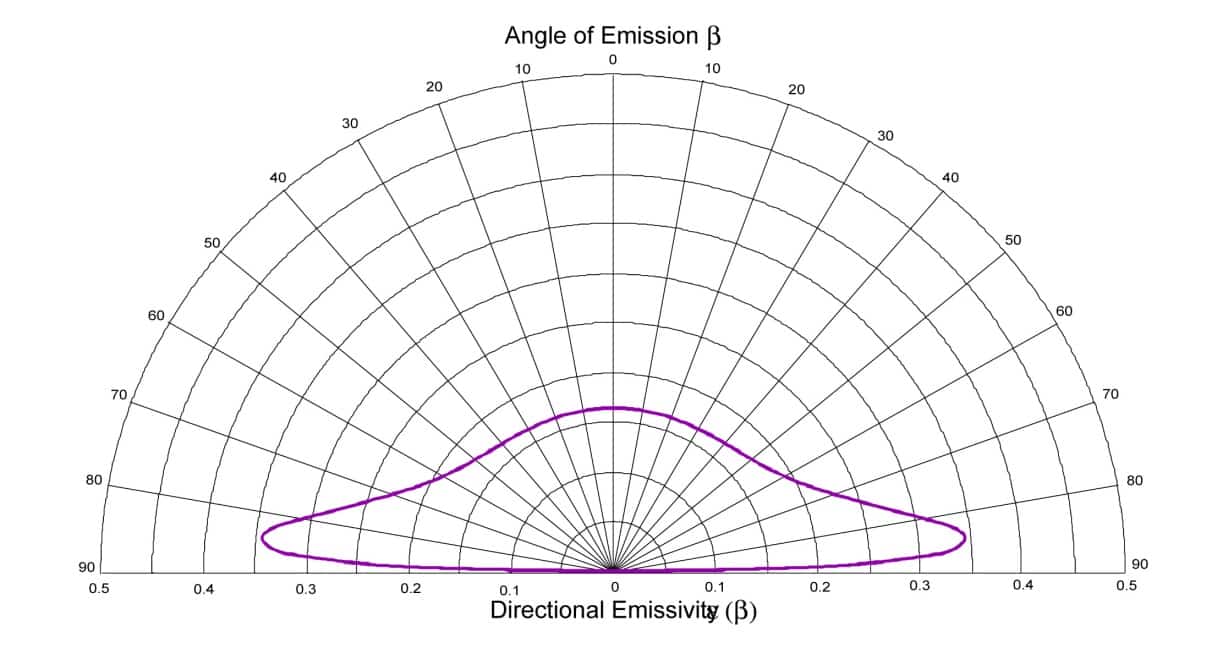
Figure 5
Emissivité directionnelle en fonction de l’angle pour un métal d’indice de réfraction : n = 5.7+9.7. i
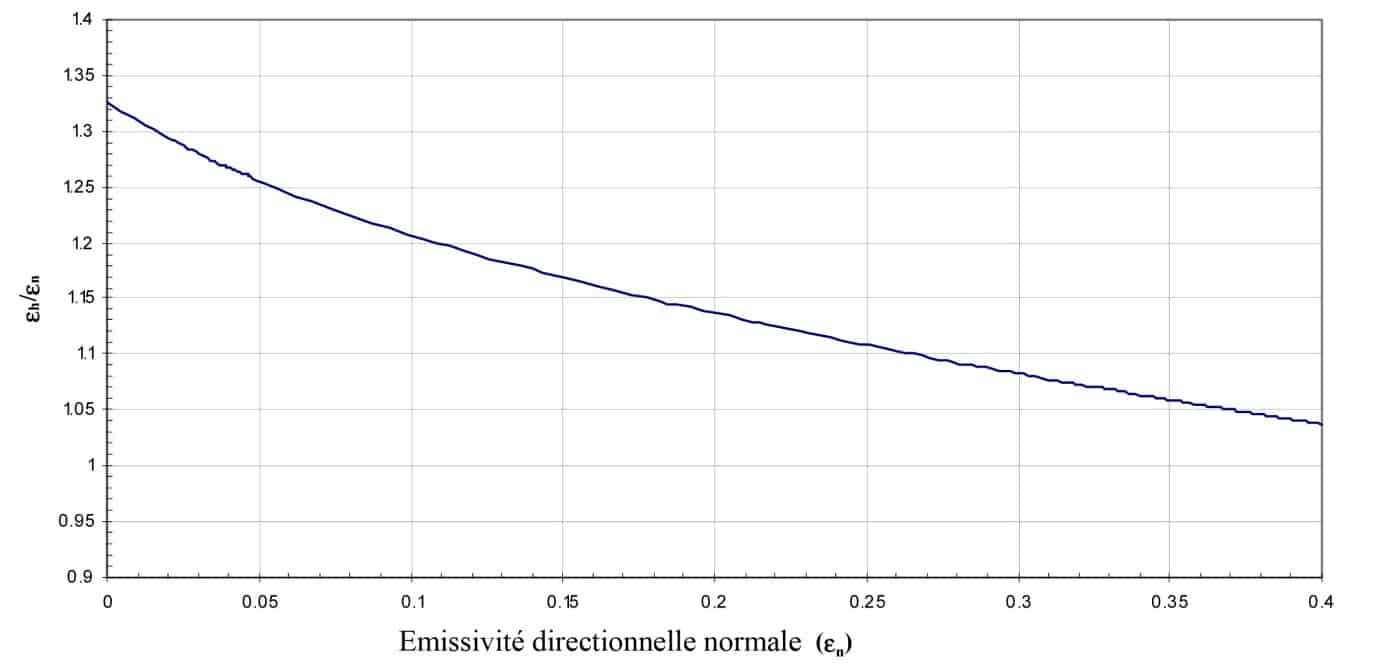
Figure 6
Rapport entre l’émissivité hémisphérique et l’émissivité directionnelle normale en fonction de l’émissivité directionnelle normale pour les conducteurs lisses (2)
Pour les conducteurs, deux paramètres, n0 et χ peuvent varier. La Figure 6 montre une courbe théorique obtenue en faisant varier la partie imaginaire de l’indice. Pour les cas plus complexes et surtout pour les surfaces rugueuses des études expérimentales ont permis de tabuler des valeurs.
2.4 Relation entre l’émissivité directionnelle normale et l’émissivité hémisphérique
On mesure fréquemment pour des questions de facilité l’émissivité directionnelle en incidence quasi normale. Cependant il est souvent nécessaire d’obtenir l’émissivité hémisphérique. Celle-ci est l’intégration sur l’ensemble des angles solides utile de l’émissivité directionnelle.
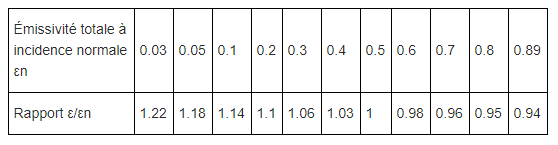
Si l’on ne peut mesurer celle-ci sur l’ensemble des incidences on doit pouvoir déduire l’émissivité hémisphérique de l’émissivité directionnelle en incidence quasi normale. Ce calcul est possible théoriquement pour les dioptres lisse de diélectriques car l’émissivité ne dépend que de l’indice normal (Figure 1). Les valeurs du Tableau 1 sont issues de la norme ISO 12898. Elle est destinée à la mesure de l’émissivité des vitrages.
Tableau 1 Facteurs permettant de calculer l’émissivité totale hémisphérique à partir de εn pour une surface diélectrique lisse
Quelques études remarquables ont permis de documenter ce coefficient ε∩/εn. Pour les surfaces lisses à faible émissivité (typiquement les métaux). Rubin et Hartmann ont utilisé des couches d’argent et In2O3 sur du verre. Une expression analytique a été obtenue en utilisant les données expérimentales et les relations de Kramer Kroning :
Pour les diélectriques pour lesquels l’émissivité εn est comprise entre 0.68 et 0.98 une autre expression est utilisée :
Ces données sont regroupées et enrichies dans deux rapport de recherche européen. Elles ont permis de fournir les données nécessaires à la rédaction de la norme ISO 12898.
Ces donnes sont tracées dans la . La courbe légendée Métaux correspond à l’équation (14), celle légendée Diélectrique à l’équation (15). Les valeurs tabulées dans la norme ISO 13898 sont aussi portées dans ce graphique.
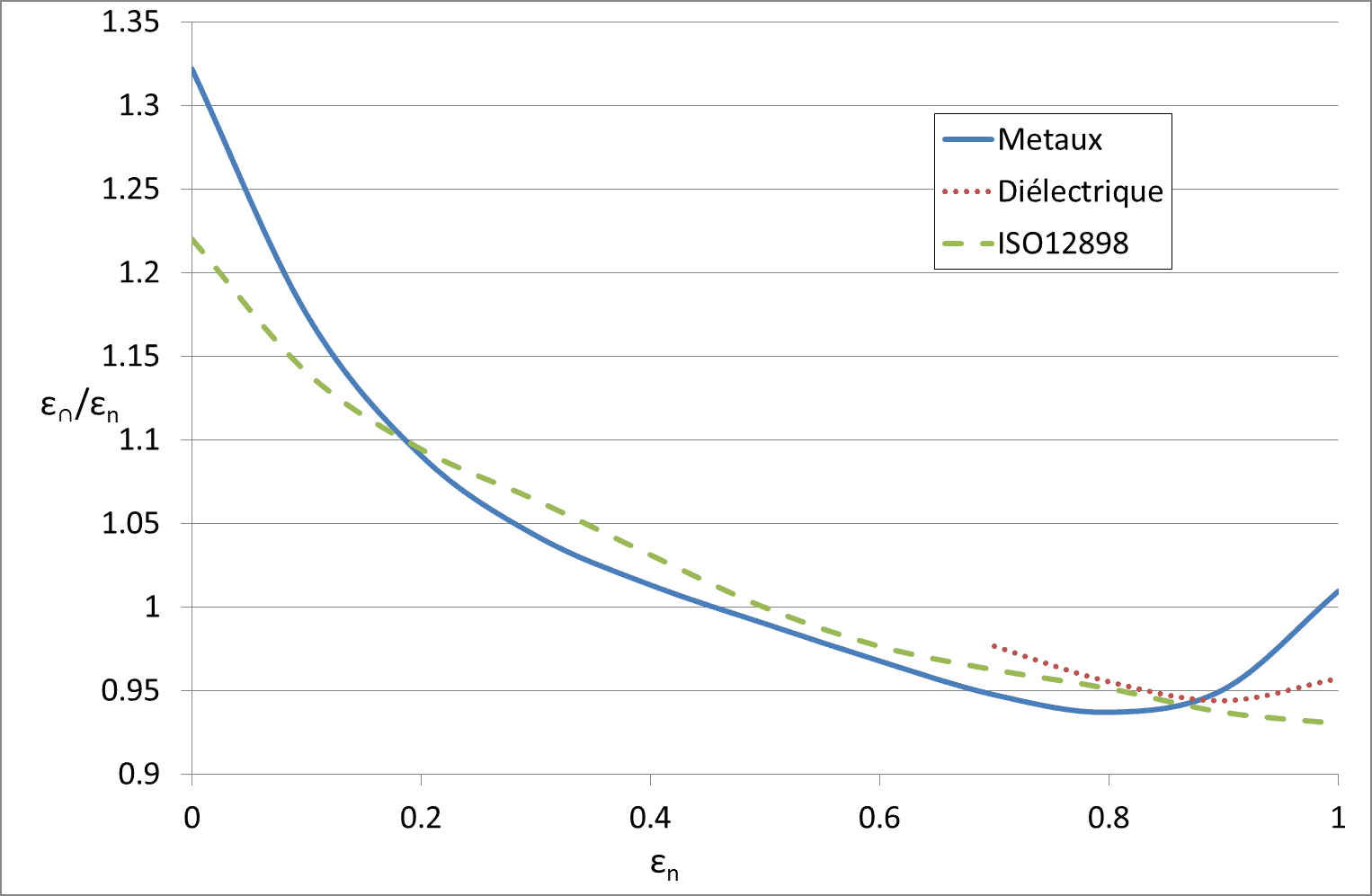
Figure 7
Rapport entre ε et εn suivant les différentes sources
3. Les différentes méthodes de mesure de l’émissivité thermique
3.1 Classification des méthodes
Dans ce chapitre, nous abordons les méthodes de mesure de l’émissivité. Elles ont été classées suivant le principe physique de la mesure. Nous avons séparé les méthodes dites directes des méthodes dites indirectes. Les méthodes directes sont celles où l’on mesure directement la puissance rayonnée par la surface : ce sont les méthodes calorimétriques et radiométriques.
Les méthodes indirectes sont celles où les propriétés des surfaces dans le domaine spectral de l’infrarouge sont déduites des propriétés optiques par réflectométrie : c’est le cas de toutes les autres méthodes. Tous les appareils commerciaux utilisent ces méthodes indirectes d’une manière ou d’une autre. Les méthodes directes ne sont limitées que par le dispositif expérimental utilisé. Les méthodes indirectes souffrent de biais intrinsèques à la méthode de mesure elle-même.
3.2 Méthode calorimétrique
La méthode calorimétrique permet d’évaluer les transferts radiatifs sans négliger aucune incidence ni aucune longueur d’onde. Elle consiste à effectuer un bilan énergétique des pertes radiatives de l’échantillon étudié quand celles-ci sont les seules en jeu. C’est une méthode directe et absolue, c’est-à-dire qu’elle ne nécessite pas de référence d’émissivité étalon pour
obtenir l’émissivité de l’échantillon. Cette méthode reste lourde. En effet, pour éliminer les transferts par conduction et convection, on doit placer l’échantillon sous atmosphère réduite (typiquement 10−5 mbar). On chauffe l’échantillon et on le maintient à la température à laquelle on souhaite connaître l’émissivité. Pour maintenir sa température, on doit lui fournir
une puissance :
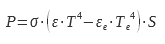
où P est la puissance dissipée par l’échantillon, ε son émissivité, σ la constante de Stefan- Boltzmann, T la température de l’échantillon, εe l’émissivité de l’enceinte, Te la température de l’enceinte et S la surface émissive de l’échantillon.
La puissance nécessaire pour maintenir l’échantillon à la température à laquelle on souhaite connaitre l’émissivité est fournie de manière électrique sous forme d’effet Joule. La Figure 1 Figure 8 représente schématiquement un dispositif de mesure de l’émissivité par la méthode calorimétrique. L’enceinte (F) est maintenue sous vide à l’aide d’un dispositif de pompage relié à l’enceinte par la tuyauterie A.
Les fils électriques d’alimentation et de mesure (B) sont reliés à l’échantillon par un bornier C. Celui-ci sert de garde pour éviter les pertes par conduction. La température de ce bornier est maintenue et régulée à la même température que l’échantillon. De cette manière, la puissance dissipée par conduction par les fils électriques d’alimentation et de mesure entre le bornier et l’échantillon est nulle pour cause d’absence de gradient de température.
Le disque-échantillon de surface rayonnante connue est suspendu dans l’enceinte. L’enceinte E est un cryostat calorifugé généralement rempli d’azote liquide. L’hélium est utilisé quand on souhaite mesurer des émissivités à des températures basses (inférieures à 250K) pour l’industrie spatiale. Un tel dispositif est décrit dans Fabron et Meurat.. L’enceinte F est recouverte à l’intérieur d’un revêtement d’émissivité élevée et d’émissivité spectrale variant peu avec la longueur d’onde. Le choix de la température du cryostat est guidé par la nécessité d’avoir ε.T4 ≫ εe.Te4. La température idéale doit permettre d’obtenir un biais bien inférieur à l’incertitude de mesure du dispositif. A partir de la relation 16, on peut en déduire l’émissivité:
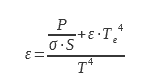
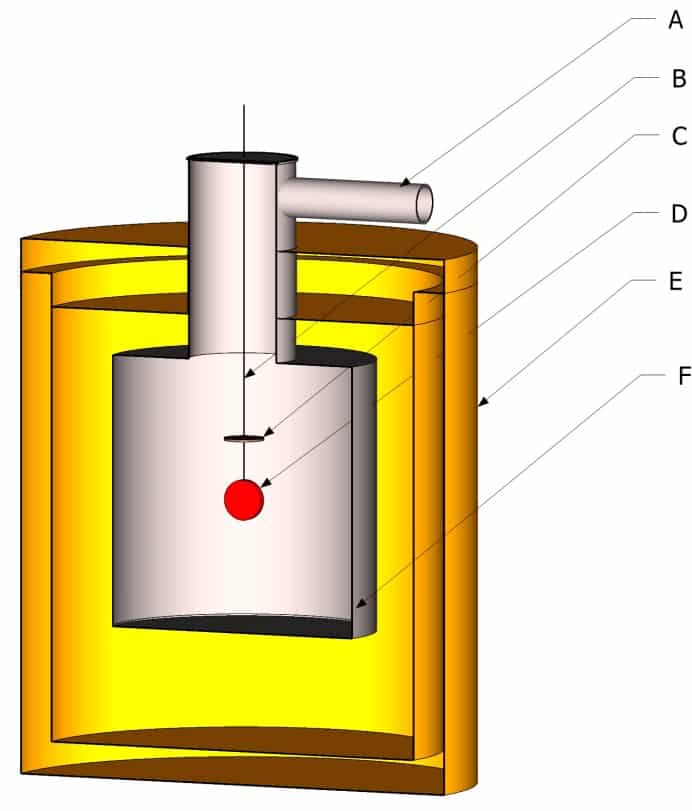
Figure 8
Schéma de principe de la méthode calorimétrique
La méthode calorimétrique est la seule à permettre une détermination directe de l’émissivité totale hémisphérique. L’intégralité du rayonnement est prise en compte. Le fait qu’elle ne nécessite pas de référence ou d’étalon d’émissivité en fait une méthode de référence.
Cette méthode reste cependant lourde et longue à mettre en œuvre. Il serait difficile de constituer une base de données d’émissivité avec cette seule méthode. La source d’incertitude principale est la mesure de température de surface. Celle-ci peut être extrapolée en mesurant le gradient de température à l’intérieur de l’échantillon à l’aide de différents capteurs .
Par ailleurs, il est nécessaire d’avoir des échantillons calibrés en taille pour s’insérer dans le dispositif de mesure. D’autres dispositifs plus simples sont décrits dans Moghaddam, Lawler et Currano.
3.3 Méthode radiométrique
3.3.1 Méthode par mesure directe du flux/de la luminance
Cette méthode consiste à comparer la luminance d’un échantillon à celle d’un corps noir porté à la même température. Le dispositif est décrit Figure 9Figure 1. Sur cette figure, l’échantillon A est porté à la température à laquelle on souhaite mesurer l’émissivité. Celui-ci est placé dans une enceinte refroidie B avec les mêmes conditions de température que pour la méthode calorimétrique (ε.T4 ≫ εe.Te4). Un corps noir E porté à la même température que l’échantillon est la référence de luminance.
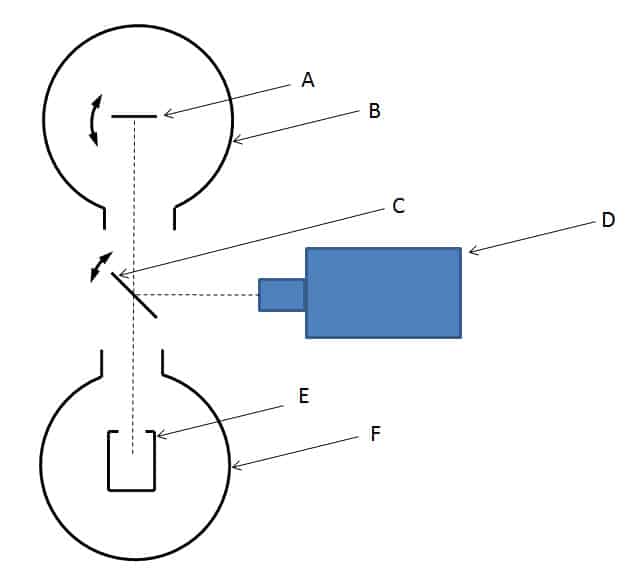
Figure 9
Méthode radiométrique
On mesure successivement la luminance du corps noir et celle de l’échantillon grâce au miroir basculant C. Le rapport entre ces deux luminances donne l’émissivité. Le corps noir est placé dans une enceinte calorifugée sans condition de température. Il est possible de faire la mesure avec un corps noir ayant une température différente de celle de l’échantillon. Dans ce cas un rapport entre les températures à la puissance 4 s’applique.
On mesure les deux luminances grâce au détecteur D. Celui-ci peut être un détecteur infrarouge large bande (comme une thermopile) pour mesurer l’émissivité totale. Ce détecteur peut être muni d’une roue porte-filtre pour mesurer l’émissivité spectrale pour différentes longueurs d’onde.
L’ensemble des dispositifs de mesure d’émissivité par comparaison à un corps noir du NIST (National Institute of Standards and Technology, Gaithersburg, Maryland, Etat-Unis) est présenté dans Novel method for measurement of total hemispherical emissivity. Dans ce dispositif il n’y a pas de miroir basculant, le système de détection est déplacé en face des surfaces à mesurer et des corps noirs de référence au moyen d’un chariot. Ce dispositif fait référence dans le domaine pour les mesures d’émissivité pour des températures allant de 600K à 1400K .
L’émissomètre décrit par Campo, Esquisabel, Fernandez et Telloutilise un spectromètre infrarouge à transformée de Fourier. La luminance est donc mesurée dans une seule direction, on mesure ainsi une émissivité directionnelle. Pour mesurer différentes incidences et remonter à l’émissivité hémisphérique, certains dispositifs permettent de faire tourner l’échantillon : c’est le cas du dispositif décrit dans New experimental device for infrared spectral directional emissivity measurements in a controlled environment. Le spectromètre peut aussi être remplacé par un monochromateur comme le dispositif décrit dans Measurement of Spectral Directional Emissivity of Materials and Coatings in the Infrared Region of Spectrum.
La mesure radiométrique à température ambiante nécessite de placer l’échantillon dans un cryostat à très basse température et sous vide pour éviter la condensation. Un dispositif original évitant ce problème est décrit dans A Simple High-Sensitivity Radiometer in the Infrared for Measurements of the Directional Total Emissivity of Opaque Materials at Near-Ambient Temperatures.
Le principe reste le même, cependant les mesures sont effectuées à température ambiante, le flux mesuré est ensuite corrigé à partir des mesures de température de l’enceinte et du chopper. Cela simplifie grandement le dispositif, mais introduit des sources d’incertitude supplémentaires.
3.3.2 Méthode radiométrique périodique
La méthode radiométrique périodique consiste à moduler faiblement la température de l’échantillon autour de la température où l’on désire connaître l’émissivité. Ainsi, on peut séparer le flux réfléchi du flux propre de l’échantillon. C’est le principe de la méthode radiométrique modulée.
Pour obtenir l’émissivité, on doit comparer le flux mesuré à celui d’une surface d’émissivité connue. Une autre méthode consiste à moduler aussi une source hémisphérique à une fréquence différente de la fréquence modulation de l’échantillon. En effectuant la mesure sur deux échantillons inconnus, on peut obtenir la valeur de l’émissivité et de la réflectivité. Cette méthode ne nécessite pas de référence d’émissivité pour effectuer la mesure. La méthode radiométrique périodique est détaillé dans [20].
3.4 Méthodes Réflectométriques
La méthode réflectométrique consiste à mesurer le coefficient de réflexion hémisphérique directionnel ou le coefficient de réflexion directionnel hémisphérique afin de calculer l’émissivité directionnelle pour une direction équivalente à celle utilisée pour mesurer le coefficient de réflexion. Ce calcul se base sur la loi de Kirchhoff (2). On peut énoncer cette loi ainsi : pour une surface opaque en équilibre thermique avec son environnement, on peut écrire pour une longueur d’onde λ :
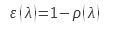
L’équilibre thermique impose une température identique pour l’environnement et pour la surface en question. On peut élargir
cette relation à une plage de longueur d’onde.
On peut calculer ce coefficient de réflexion soit en mesurant la réflectance pour toutes les longueurs d’onde et en effectuant l’intégration pondérée par l’émittance du corps noir, soit en s’assurant que l’on mesure la réflectance avec une source lumineuse ayant la même répartition spectrale énergétique que le corps noir à la température considérée. Il faut en outre s’assurer que le détecteur infrarouge utilisé possède une réponse suffisamment constante dans le domaine spectral considéré.
A condition que la réflectance spectrale ne varie pas avec la température, on peut calculer cette réflectance sans se soucier de la température de l’échantillon. Nous allons voir plusieurs méthodes de mesure d’émissivité à partir de la mesure de réflectance.
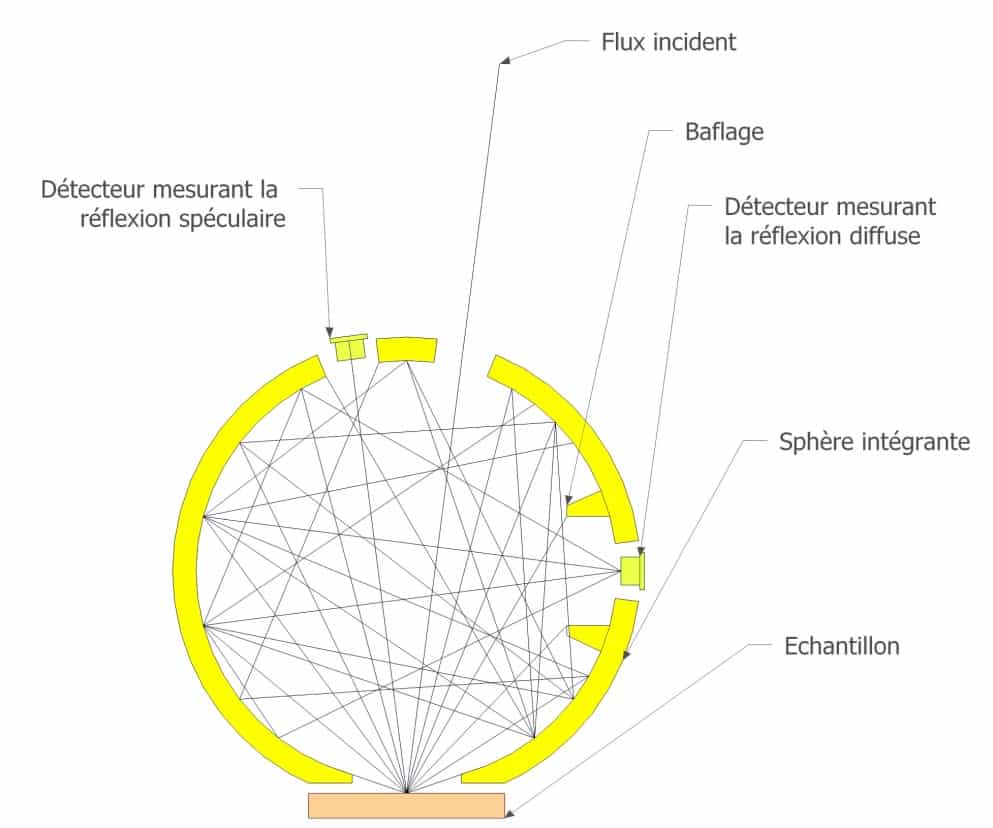
Figure 10
Schéma d’un dispositif de mesure de la réflexion directionnelle hémisphérique par la méthode de la sphère intégrante
3.4.1 Méthodes à miroir ?
3.4.2 Méthode par sphère intégrante
La Figure 10 montre le fonctionnement d’une sphère intégrante. Celle-ci doit être recouverte intérieurement d’un revêtement réfléchissant et diffusant. On éclaire l’échantillon grâce à une source infrarouge dans une direction donnée proche de la normale. L’angle d’incidence dans les sphères intégrantes commerciales est compris entre 8 et 12 degrés. Une fois que la lumière a atteint l’échantillon, celle-ci est diffusée dans toutes les directions selon l’indicatrice de réflectance du matériau.Après de multiples réflexions, la lumière atteint le détecteur placé sur le côté. Ainsi le détecteur mesure en théorie la quasi-totalité du flux réfléchi par l’échantillon. Un système de bafflage évite que le détecteur ne voie directement l’échantillon pour ne pas perturber la mesure. Un détecteur peut être placé symétriquement à la source pour mesurer la réflexion spéculaire.
Celui-ci est optionnel, et sur certaines sphères on peut mettre à l’emplacement de la réflexion spéculaire soit une portion de surface diffusante de même nature que la sphère, soit laisser ouvert celui-ci. Dans le premier cas, on mesure l’ensemble du flux réfléchi (diffus et spéculaire) et dans l’autre cas seulement le flux diffus.
Par soustraction, on peut obtenir le coefficient de réflexion spéculaire. Pour effectuer une mesure de coefficient de réflexion, il est nécessaire d’étalonner le dispositif avec une référence de réflectance. On utilise le même type de revêtement que celui utilisé pour la sphère. C’est généralement une surface métallique sablée ou microbillée recouverte d’une couche d’or. Un dispositif de ce type est utilisé au NIST. Il est décrit dans Infrared diffuse reflectance instrumentation and standards at NIST.
3.4.3 Méthode utilisant une source modulée
Précédemment, pour la méthode radiométrique, quand on souhaitait mesurer le flux émis par la surface il fallait s’affranchir du flux provenant de l’environnement radiatif autour de l’échantillon. Celui-ci était donc placé dans une enceinte refroidie à une température Te, de manière à assurer σ.T4>>σ.Te4. Cette condition contraignante est toutefois facile à obtenir grâce à une enceinte refroidie à l’eau pour des températures d’échantillon de l’ordre de 1000K. Cependant lorsque l’on veut mesurer une émissivité à température ambiante, il est nécessaire de refroidir l’enceinte à des températures cryogéniques. Pour éviter cette complexité supplémentaire on peut moduler la température de l’échantillon à mesurer autour de la température à laquelle on souhaite connaître l’émissivité. Dans ce cas on détecte le flux modulé émis et on le compare à amplitude de modulation égale à celui émis par une surface de référence. Quand il n’est pas possible de moduler la température de l’échantillon, on peut utiliser une méthode réflectométrique et moduler le flux utilisé pour mesurer le facteur de réflexion. Ces méthodes sont décrites dans Infrared emissivity measurement device : Principle and applications. et un exemple précis de réalisation dans Développement de techniques de mesure de l’émissivité de matériaux opaques à température ambiante.
Pour séparer le flux propre de l’échantillon du flux réfléchi, on envoie sur celui-ci un flux hémisphérique modulé en fréquence. Le principe consiste à produire un flux infrarouge hémisphérique modulé autour de l’échantillon étudié et de mesurer, dans une direction, le flux réfléchi par la surface du matériau à l’aide d’une thermopile. Le schéma de la Figure 11 montre le principe du dispositif. On étalonne auparavant le dispositif grâce à un matériau de référence connu. La Figure 12 montre le schéma de l’appareil développé au CERTES ainsi qu’une photo de l’instrument. La cavité est constituée d’un cube creux en aluminium ouvert par le bas. La température des parois est modulée grâce à des éléments à effet Peltier. La mesure du flux réfléchi se fait à travers un orifice pratiqué au sommet du dispositif au moyen d’une thermopile munie d’une lentille en KRS5.
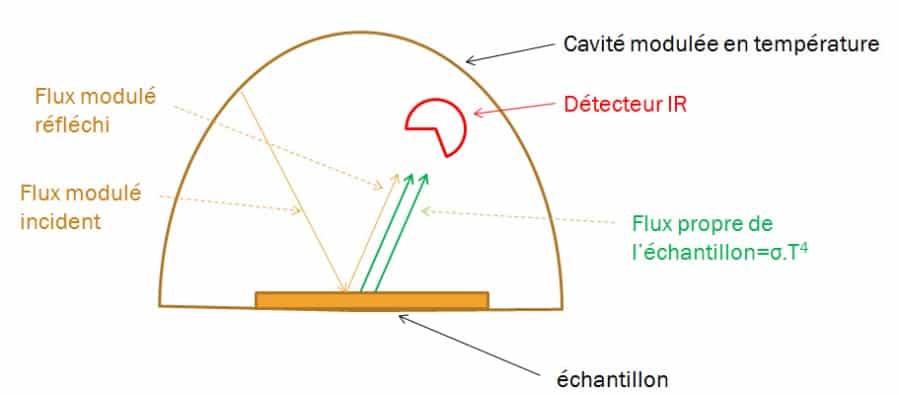
Figure 11
Principe de la méthode de mesure réflectométrique avec une source modulée
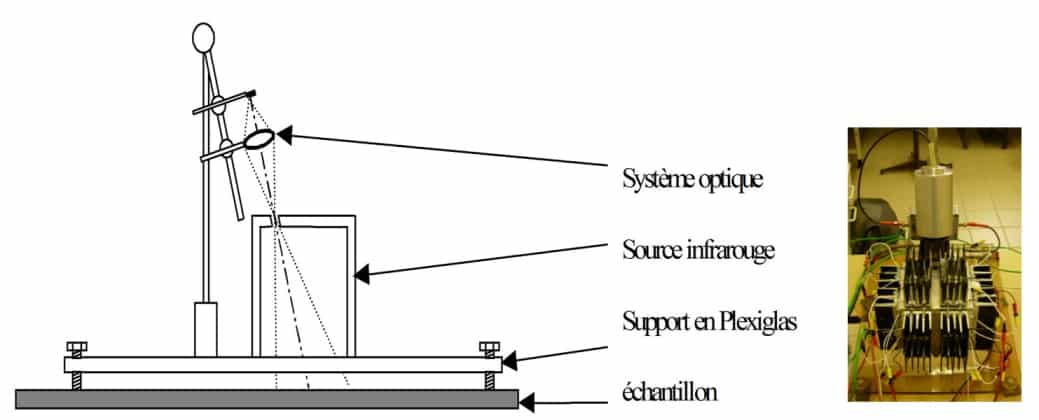
Figure 12
Schéma et photo du dispositif de mesure développé au CERTES
Une autre méthode permettant de moduler le flux hémisphérique est d’utiliser un chopper tridimensionnel. Ce dispositif a été breveté par l’université ParisXII. Ce dispositif est présenté ci dessous
EM3 de THEMACS Ingénierie :
Le principe de cet appareil est celui décrit au précédement. Il consiste à moduler une source de rayonnement hémisphérique par des volets mobiles. Cela évite de moduler la cavité en température ce qui est très lent. Le schéma Figure présente le principe de modulation. La source est le cylindre B chauffé à une température légèrement supérieure à la température ambiante.
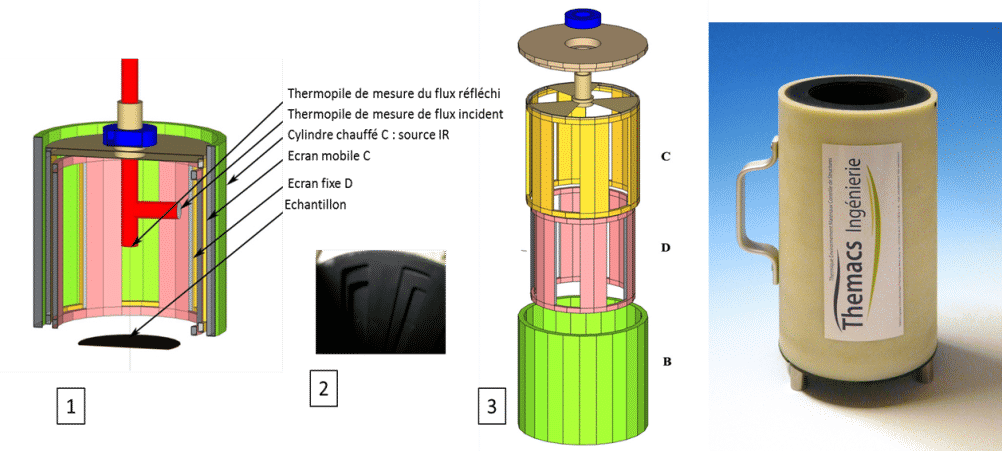
Figure 13
Emissomètre EM3 de THEMACS Ingénierie
Le cylindre mobile C et l’écran fixe D occultent la source hémisphérique à une fréquence de 10Hz pour la paroi cylindriques (présence de 6 fenêtres) et de 5Hz pour la partie sommitale (présence de 3 fenêtres). De cette manière, il est possible de différencier un matériau spéculaire d’un matériau diffusant. Une thermopile mesure le flux incident et une autre le flux réfléchi. Le ratio du flux réfléchi ne dépend pas du niveau émis par la source.
Cet émissomètre doit être préalablement calibré grâce à deux surfaces d’émissivité connues. On prend généralement une surface très fortement émissive (peinture Nextel, 3M™) et une surface très faiblement émissive (aluminium diffusant). La Figure montre le schéma général (1), un détail des volets mobiles et fixe, et de la source recouverts de peinture Nextel (3M™) (2), une vue éclaté du dispositif (3) et une photo de l’appareil. Le dispositif est portable et doit être connecté à un ordinateur permettant de démoduler les signaux par FFT.
4 Pour aller plus loin
Plusieurs documents généraux peuvent compléter cette étude sur les mesures d’émissivité. On peut citer notamment :
– « Measurement of Thermal Radiation Properties of Solids », [13]. Ce document est l’ensemble des interventions d’un congrès de 1962 sur les propriétés radiatives des matériaux. Malgré l’ancienneté de cette publication, elle recense de manière très complète un grand nombre de dispositifs de mesure de l’émissivité utilisé dans le domaine de l’aéronautique. Si les technologie ont fortement évolués depuis, les principes de mesure de ces dispositif restent d’actualité.
– « Measurement Techniques for Thermal Radiation Properties », [12]. De la même manière, ce document fait l’état des lieux de la technique en 1990. De nouveaux dispositifs sont décrits.
– « Spacecraft Thermal Control Coatings References », [11]. Ce document de référence de la NASA qui est un des plus récents décrit dans un premier temps les grandeurs mesurées. Ensuite, un calcul théorique liant les indices complexes des matériaux et les propriétés radiatives est exposé. Les diverses méthodes de mesure sont ensuite décrites. En fin de document, des mesures sur des matériaux fréquemment utilisés dans le domaine de l’aérospatiale sont présentées. Ce document, comme le premier cité plus haut, décrit aussi les propriétés optiques dans le visible ; celles-ci sont également importantes à connaître pour déduire l’équilibre thermique d’un satellite soumis au rayonnement solaire.
5 Bibliographie
- Maldague, X.P. Theory and practice of infrared technology for non destructive testing,. s.l. : Ed. Wiley, 2001.
- Kauder, L. Spacecraft Thermal Control Coatings References, NASA-TP-2005-212792,. 2005.
- P. Lorrain, D.R. Corson. Champs et ondes électromagnétiques. s.l. : Armand Collin.
- Rubin, M., Arasteh, D. et Hartmann, J. A correlation between normal and hemispherical emissivity of low emissivity coatings on glass. s.l. : Int. Comm. Heat Mass Transfer, 1987.
- Blain, B. J. et Douglas, R. W. Infra-red optical constants of glasses. 1965.
- D. Janssen, J. Lohrengel. investigation and development of a method for the measurement of the emissivity of glass. s.l. : BCR european community, 1991. EUR 13487 EN.
- GEOTTI-BIANCHINI, F. Total hemispherical emissivity of coated glass. s.l. : European community, 1993. EUR 14758 EN.
- C. Fabron, A. Meurat. Measurement of total hemispheric emissivity at low temperature. s.l. : International Symposium on nvironnemental Testing for Space Program, Liège, Belgium, 2001.
- J. Hameury, B. Hay, J. R. Filtz. Measurement of Total Hemispherical Emissivity Using. s.l. : Int. J. Thermophys, 1607, 2007.
- S. Moghaddam, J. Lawler, J. Currano. Novel method for measurement of total hemispherical emissivity. s.l. : J. Thermophys. Heat Transfer, 2007.
- A. Mazikowski, K .Chrzanowski. Non-contact multiband method for emissivity measurement. s.l. : Infrared Phys. Technol., 91, 2003.
- L. Hanssen, S. Mekhontsev, V. Khromchenko. Infrared Spectral Emissivity Characterization Facility at NIST, . s.l. : Thermosense XXVI, edited by Douglas D. Burleigh, K. Elliott Cramer,G. Raymond Peacock,Proc. of SPIE Vol. 5405, SPIE, Bellingham,WA, 2004.
- L. Del Campo, R.B. Perez-Saez, X. Esquisabel, I. Fernandez, M.J. Tello. New experimental device for infrared spectral directional emissivity measurements in a controlled environment. s.l. : Review Of Scientific Instruments, vol. 77, 113111, 1-8, 2006.
- V. Vitkovskii, V. G. Gorshenev, Y. F. Potapov. Measurement of Spectral Directional Emissivity of Materials and Coatings in the Infrared Region of Spectrum. s.l. : Thermal Engineer , 245-248 Vol. 56-3, 2009.
- A. Pantinakis, N. Kortsalioudakis. A Simple High-Sensitivity Radiometer in the Infrared for Measurements of the Directional Total Emissivity of Opaque Materials at Near-Ambient Temperatures. s.l. : International Journal of Thermophysics, 1843-1854 Vol. 22-6, 2001.
- L.M. Hanssen, S. Kaplan. Infrared diffuse reflectance instrumentation and standards at NIST. s.l. : Anal. Chim. Acta, 289 , 1999.
- D. Especel, S. Matteï. Total Emissivity Measurement Without Use of an Absolute Reference. s.l. : Infrared Phys. Technol., 777-784 vol.37, 1996.
- L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau. Infrared emissivity measurement device : Principle and applications. s.l. : Meas. Sc. Tech., 2950, 2006.
- M.Siroux. Développement de techniques de mesure de l’émissivité de matériaux opaques à température ambiante. Approches radiométrique et calorimétrique en régime périodique. s.l. : Thèse Université Paris 12, 1996.
Notre équipe vous conseille pour répondre au mieux à vos attentes