Bedeutung und Grenzen von Spektralmessungen
Bedeutung und Grenzen spektraler Messungen für die Emissionsgradmessung
Autoren :
Jean-Pierre MONCHAU, THEMACS Ingénierie, 2bis rue Alfred Nobel, 77420 Champs sur Marne,monchau@themacs.fr
Laurent IBOS, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, ibos@u-pec.fr
Mario MARCHETTI, CEREMA, Laboratoire Régional de Nancy,71, rue de la Grande Haie – 54510 Tomblaine,Mario. Marchetti@cerema.fr
Jean DUMOULIN, IFSTTAR, Dépt. CoSys, Route de Bouaye, 44344 Bouguenais Cedex, jean.dumoulin@ifsttar.fr
Vincent FEUILLET, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, vincent.feuillet@u-pec.fr
Emissionsgrad
Der Emissionsgrad
st eine thermophysikalische Eigenschaft von Materialien, die für die Quantifizierung des Wärmeaustauschs durch Strahlung wichtig ist. Er ist auch für die Messung der Oberflächentemperatur anhand einer Leuchtdichtemessung, beispielsweise durch Infrarot-Thermografie, von entscheidender Bedeutung.
Letztere Technik findet mit der Verbreitung von Wärmebildkameras mit Mikrobolometer-Arrays zunehmend Anwendung. Die Messung des Emissionsgrades bei Raumtemperatur erfolgt in der Regel indirekt nach dem Kirchhoffschen Gesetz, das den Emissionsgrad mit dem Reflexionsgrad eines undurchsichtigen Materials in Beziehung setzt. Es gibt mehrere kommerzielle Geräte, die jedoch Messabweichungen aufweisen. Um diese Fehler zu korrigieren, muss das spektrale Verhalten des Materials bekannt sein.
Die Messung des spektralen Reflexionsfaktors mit einem Fourier-Transform-Infrarotspektrometer (FTIR), das mit einer Ulbrichtkugel ausgestattet ist, ermöglicht es, diese Informationen zu erhalten. Die spektrale Begrenzung von Ulbrichtkugeln (im Allgemeinen 1-20 µm) macht jedoch den Einsatz eines Emissometers erforderlich, das einen größeren Spektralbereich abdeckt.
CERTES hat ein Messprotokoll entwickelt, das beide Techniken (Breitband und Spektral) kombiniert, um einen unverfälschten Emissionsgradwert zu erhalten, der um Temperaturschwankungen der Quelle korrigiert ist. Diese Methode wurde erfolgreich für verschiedene Materialien getestet, insbesondere für Keramiken wie Aluminiumoxid (Al2O3), die starke Schwankungen der Reflexion im Bereich von 1 bis 20 µm aufweisen. Diese Ergebnisse werden in diesem Artikel vorgestellt.
Definition der Emissivität
Max Planck hat die spektrale Emittanz eines idealen Körpers, eines sogenannten schwarzen Körpers, mithilfe der Quantentheorie theoretisch bestimmt (Abbildung 1). Reale Oberflächen strahlen ähnlich, aber die Emittanz wird durch einen dimensionslosen Koeffizienten, die Emissivität, gewichtet.
Dieser Koeffizient hängt vom Material, seiner Temperatur, der Wellenlänge und dem Einfallswinkel (hier dem Emissionswinkel) ab. Thermotechniker bevorzugen die Verwendung eines integrierten Koeffizienten über das gesamte Spektrum und für alle Einfallswinkel, der als hemisphärische Gesamtemissivität bezeichnet wird, um beispielsweise die durch Strahlung von einer Oberfläche verlorene Wärmemenge quantifizieren zu können.
Die Schwierigkeit besteht daher darin, diesen Koeffizienten zu bestimmen, ohne Wellenlängen oder Einfallswinkel zu vernachlässigen.
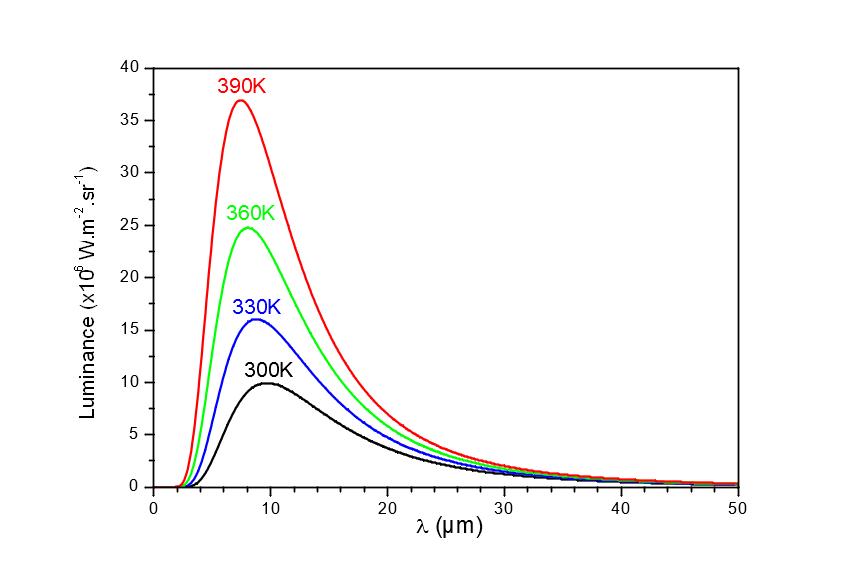
Abbildung 1
Leuchtdichte eines schwarzen Körpers L(λ) für verschiedene Temperaturen T
Zur Messung der Emissivität gibt es viele Ansätze, die wir in zwei Kategorien einteilen können: Die direkten Methoden messen die energetische Strahlung der untersuchten Oberfläche, während die indirekten Methoden die Emissivität aus anderen optischen Eigenschaften der Oberfläche ableiten.
Unter den direkten Methoden kann man die kalorimetrische Methode nennen, bei der die elektrische Leistung gemessen wird, die einer Probe (die sich in einem Kryostaten unter Vakuum befindet) zugeführt werden muss, um ihre Oberflächentemperatur auf der Temperatur zu halten, bei der man den Emissionsgrad ermitteln möchte. Das Nationale Labor für Metrologie und Prüfung (LNE) verfügt über einen Messstand dieses Typs [3].
Eine andere Methode, die als radiometrisch bezeichnet wird, besteht darin, die von der Oberfläche des Materials ausgehende Wärmestrahlung zu messen. Diese Messung kann in Abhängigkeit vom Winkel erfolgen, um die Richtungsemissivität zu erhalten, und in Abhängigkeit von der Wellenlänge (z. B. mit einem FTIR-Spektrometer), um die spektrale Richtungsemissivität zu erhalten. Das CEMHTI-Gerät (Extreme Conditions and High Temperature Materials and Irradiation) ermöglicht diese Art der Messung bei sehr hohen Temperaturen [4].
Für die Messung der Emissivität bei Umgebungstemperatur ist der Fluss zu gering, um mit guter Genauigkeit gemessen werden zu können: Dies ist der bevorzugte Bereich indirekter Methoden. Diese nutzen das Kirchhoffsche Gesetz, das die Emissivität ε mit dem Reflexionsgrad ρ und dem Transmissionsgrad τ für eine bestimmte Wellenlänge λ in Beziehung setzt :
![]()
wobei die Emissivität gleich der Absorptionsfähigkeit ist. Bei einem undurchsichtigen Material ist die Emissivität daher gleich :
![]()
Um die Gesamtemissivität zu erhalten, müssen wir daher den spektralen Reflexionsfaktor (ich sehe dieses Wort zum ersten Mal) addieren, gewichtet mit der spektralen Energieverteilung des schwarzen Körpers bei der Temperatur, bei der man die Emissivität ermitteln möchte :
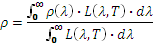
Die andere Lösung besteht darin, den globalen Reflexionsfaktor zu messen, indem die Oberfläche mit einer Lichtquelle beleuchtet wird, die diese Energieverteilung aufweist.
Mehrere handelsübliche Geräte zur Messung der Emissivität verwenden diese Methode. Ihr Hauptvorteil besteht darin, dass sie die Reflexion in einem Spektralbereich von 1 bis 50 µm messen, der 95 % der von einem schwarzen Körper bei Umgebungstemperatur (ca. 300 K) abgestrahlten Energie ausmacht. Allerdings integrieren sie den Reflexionsfaktor für eine Spektralverteilung, die sich von der Umgebungstemperatur unterscheidet.
Tatsächlich verwenden sie schwarze oder graue Körper als Infrarotquellen mit einer Temperatur über der Umgebungstemperatur. Diese Quellen haben andere Spektralverteilungen als ein schwarzer Körper bei 300 K. Dieser Unterschied in der Spektralverteilung führt zu Emissionsgradmessfehlern von bis zu 5 % bei nicht grauen Körpern. Dieser Mangel ist nichts Neues.
Tatsächlich wird er in der Norm ASTM E408-71 (Standard Test Method for Total Normal Emittance of Surface Using Inspection-Meter Techniques) erwähnt. Wir können auch auf [5] verweisen, wo diese Art von Fehler kurz erwähnt wird.
Die bei CERTES entwickelten Emissometer [1,2] verwenden Infrarotquellen, deren Temperatur sehr nahe an der Umgebungstemperatur liegt. Das Problem bleibt jedoch ungelöst, da die Modulation die Spektralverteilung der Quelle erheblich beeinflusst (siehe Kasten 1).
Um diese Unsicherheit zu beseitigen, muss die hemisphärische spektrale Richtungsreflexion gemessen werden (diese entspricht aus Gründen der Reziprozität der hemisphärischen Richtungsreflexion). Die einzigen kommerziellen Geräte, mit denen diese Messung durchgeführt werden kann, sind Ulbrichtkugeln. Sie können an FTIR-Spektrometer gekoppelt werden und ermöglichen Messungen im Spektralbereich von 1 bis 20 µm.
Was heute den Spektralbereich von handelsüblichen Ulbrichtkugeln einschränkt, ist deren Innenauskleidung. Diese muss perfekt diffus sein (Lambert’sches Verhalten). Dies ist bei Wellenlängen über 20 µm nicht mehr der Fall. Wir müssen uns daher mit diesem Spektralbereich begnügen, der nur 76 % der bei 300 K abgestrahlten Energie ausmacht. Das bei CERTES und von THEMACS Engineering verwendete Gerät ist ein Infrarotspektrometer mit Fourier-Transformation FRONTIER© der Marke Perkin-Elmer©. Das Spektrometer wird durch eine Ulbrichtkugel der Marke PIKE© ergänzt.
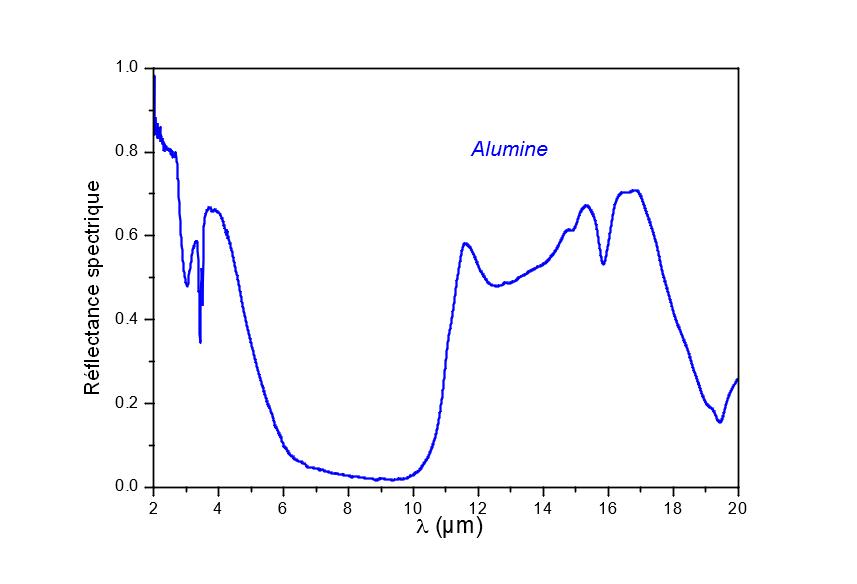
Abbildung 3
Spektraler Reflexionsfaktor als Funktion der Wellenlänge einer Aluminiumoxidprobe
Diese experimentellen Geräte sind in Abbildung 2 zu sehen. Trotz dieser Einschränkung liefert die Spektralmessung genaue Informationen über die Schwankungen der Emissivität in Abhängigkeit von der Temperatur. Durch die Kombination der beiden Techniken (Spektralmessung und Breitbandmessung) können wir zu einer exakten Emissivitätsmessung zurückkehren. Wir können diese Methode anhand von Aluminiumoxid (Al2O3) veranschaulichen:
Im Fall von Aluminiumoxid beispielsweise liegt die verwendete Probe in Form von amorpher Keramik vor. Dieser Materialtyp ist ein Lehrbuchbeispiel, da sein direktionales spektrales Emissionsvermögen um 10 µm (Abbildung 3) stark variiert, d. h. um die maximale Emission eines Körpers bei Raumtemperatur.
Dies ist bei dieser Art von Keramik häufig der Fall. Darüber hinaus können bibliografische Daten nicht verwendet werden. Tatsächlich sind die Werte der gerichteten spektralen Emissivität von Aluminiumoxid je nach Allotropie, Kristallisationsgrad, verschiedenen Wärmebehandlungen usw. sehr variabel [6].
Wenn die Temperatur der untersuchten Oberfläche von Raumtemperatur zu höheren Temperaturen variiert, verschiebt sich die maximale Leuchtdichte der Planck-Funktion L ( λ, T) um 10 µm zu kürzeren Wellenlängen. Die maximale Leuchtdichte wird für eine Wellenlänge λmax(in µm) = 3000 /T erreicht, wobei T in K angegeben ist.
Bei Aluminiumoxid hat dies zur Folge, dass die Spannung in einem spektralen Bereich mit viel höherer Emissivität zunimmt. Die Emissivität steigt daher mit der Temperatur. Wir können die Emissivität berechnen, indem wir nur das Spektralband von 1 bis 20 µm berücksichtigen. Diese Daten sind in Tabelle 1 dargestellt. Bei dieser Berechnung wird ein wichtiger Teil des nutzbaren Spektrums vernachlässigt. Der berechnete Emissivitätswert ist daher falsch.
Angesichts der Monotonie der Planck-Funktion für Wellenlängen über 20 µm bei dieser Temperatur hängen die Schwankungen des Emissionsgrades als Funktion der Temperatur jedoch nur vom Spektralband von 1 bis 20 µm ab. Da der Wert des Emissionsgrades nicht bekannt ist, können wir den Variationskoeffizienten des Emissionsgrades in Abhängigkeit von der Temperatur relativ genau ableiten. Wenn wir mit anderen Mitteln den Emissionsgrad für eine Temperatur messen können, die höher ist als die Umgebungstemperatur, können wir den Emissionsgrad bei allen Temperaturen um 300 K ableiten.
Dies ist in den Grafiken in Abbildung 4 zu sehen. Aus den Spektralmessungen (obere Grafik in Abbildung 4) können wir die Schwankungen des Emissionsgrads in Abhängigkeit von der Temperatur ableiten (untere Grafik in Abbildung 4, blaue Linie). Mit dem EM2-Emissometer von CERTES [2] (Abbildung 5) lässt sich ein unverzerrter Wert für die Emissivität ermitteln, allerdings nur bei 360 K. Aus diesen beiden Informationen leiten wir die unverzerrte Emissivität als Funktion der Temperatur ab (unteres Diagramm in Abbildung 4, rote Linie).
Abbildung 4
Spektrale Reflexion von Aluminiumoxid, oben; Berechnung der Emissivität aus Spektralmessungen und einem Breitband-Emissometer (EM2 [2]), unten.
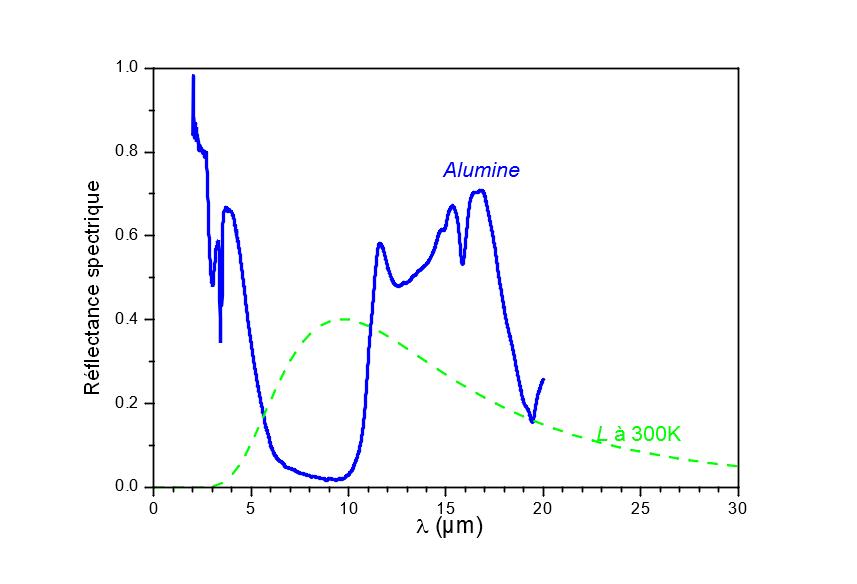
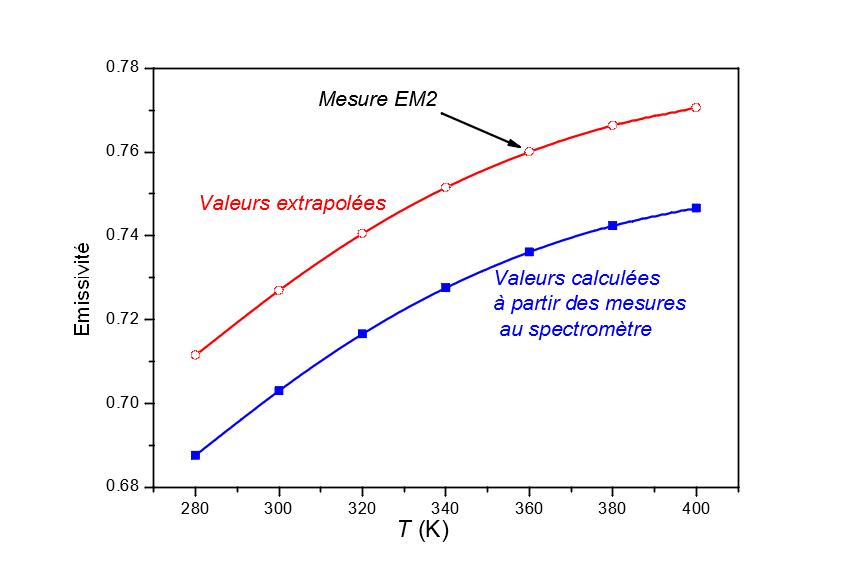

Abbildung 5
EM2-Emissionsmessgerät, entwickelt bei CERTES Breveté im Jahr 2012 (FR 2987121)
Schlussfolgerung
Die Messung der spektralen Eigenschaften von Oberflächen im Infrarotbereich ist unerlässlich, um das Strahlungsverhalten dieser Oberflächen zu kennen. Die alleinige Messung der Emissivität mit einem handelsüblichen Gerät ermöglicht es nicht, einen exakten Wert für die Emissivität zu ermitteln. Die meisten dieser handelsüblichen Geräte wurden für die Produktionskontrolle entwickelt und nicht für die Ermittlung eines gerichteten Emissivitätswertes.
Die Kombination der beiden Messmethoden und eine gute Kenntnis der Eigenschaften der verwendeten Geräte ermöglichen es, Messungen ohne systematische Fehler zu erhalten.s.
Die Nummerierung entspricht nicht der Reihenfolge des Erscheinens im Dokument.
- L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau, Infraredemissivitymeasurementdevice:
Principle and applications, Meas. Sci. Technology.17, 2950 (2006) - J-P. Monchau, M. Marchetti, L. Ibos, J. Dumoulin, V. Feuillet, Y. Candau, Infrared Emissivity Measurements of Building and Civil Engineering Materials: A New Device for Measuring Emissivity,Int. J. Thermophys., in press
- J. Hameury, B. Hay, J. R. Filtz, Measurement of Total Hemispherical Emissivity Using a Calorimetric
Technique, Int. J. Thermophys, 28, 1607 (2007) - O. Rozenbaum, D. De Sousa Meneses, Y. Auger, S. Chermanne and P. Echegut, A spectroscopic method to
measure the spectral emissivity of semi-transparent materials up to high temperature, Rev. Sci. Instrum. 70, 4020 (1999) - K.E. Nelson, E.E.Leudke, J.T.Bevans, A device for rapid measurement of total emittance, Journal of
Spacecraft and Rockets, 3, 758 (1966) - Thermophysical Properties of High Temperature Solid Materials, Vol. 4, Y. S. Touloukian Editor
BOX
Fehler aufgrund der Temperaturmodulation der Quelle
Dieser Fall betrifft Methoden, die eine reflektometrische Methode mit einer modulierten Quelle verwenden. Es wird davon ausgegangen, dass sich die spektrale Verteilung der Quelle bei geringen Temperaturschwankungen nicht wesentlich ändert. Diese Annahme ist korrekt, jedoch misst man bei diesen Methoden nicht den von der Probe reflektierten Fluss, sondern nur die Schwankungen des reflektierten Flusses.
Dies gilt auch für Quellen, die durch einen beweglichen Bildschirm (Chopper) unterbrochen werden. Tatsächlich wird in diesem Fall der Wechsel zwischen der Temperatur der Quelle und der des Bildschirms gemessen. Wenn die Temperatur T eine periodische Funktion der Zeit ist, müssen wir ihren Ausdruck als Funktion der Zeit T(t) betrachten, wobei t die Zeit ist. Das vom Detektor gemessene Signal ist gleich :
![]()
wobei L(λ,T) die Leuchtdichte des schwarzen Körpers für die Wellenlänge λ und die Temperatur T ist. Dieser Unterschied ist in Abbildung 6 dargestellt.
Da wir in diesem Fall nur an periodischen Schwankungen dieser Leuchtdichte interessiert sind, ist die Messung proportional zur vom Detektor gemessenen Spitze-Spitze-Amplitude A für Temperaturschwankungen ΔT über der Mindesttemperatur (der Einfachheit halber wird angenommen, dass die Temperatur zwischen T und T+ΔT schwankt) :
Wenn wir das dem einfallenden Fluss entsprechende Signal messen, erhalten wir den Gesamtreflexionskoeffizienten im Spektralbereich des Detektors :
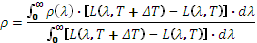
Es ist daher ersichtlich, dass in Wirklichkeit die Reflexion mit einer Quelle gemessen wird, deren Spektralverteilung der Differenz der Leuchtdichte zweier Quellen unterschiedlicher Temperatur entspricht. Diese Spektralverteilung unterscheidet sich erheblich von der Spektralverteilung eines schwarzen Körpers bei durchschnittlicher Temperatur.
Abbildung 7 zeigt die Leuchtdichte eines schwarzen Körpers bei 300 K und 360 K sowie die Differenz in der Leuchtdichte zwischen zwei schwarzen Körpern bei 300 K und 305 K. Die Kurven wurden zur besseren Lesbarkeit normalisiert. Beachten Sie, dass die spektrale Verteilung der modulierten Quelle nicht mehr dem Planckschen Gesetz folgt, sondern sich der spektralen Verteilung eines schwarzen Körpers bei 360 K annähert. Damit dieser Fehler nur einen vernachlässigbaren Einfluss hat, muss die Probe einem Graukörper um 10 µm angeglichen werden können oder die spektralen Eigenschaften der untersuchten Oberfläche müssen bekannt sein.
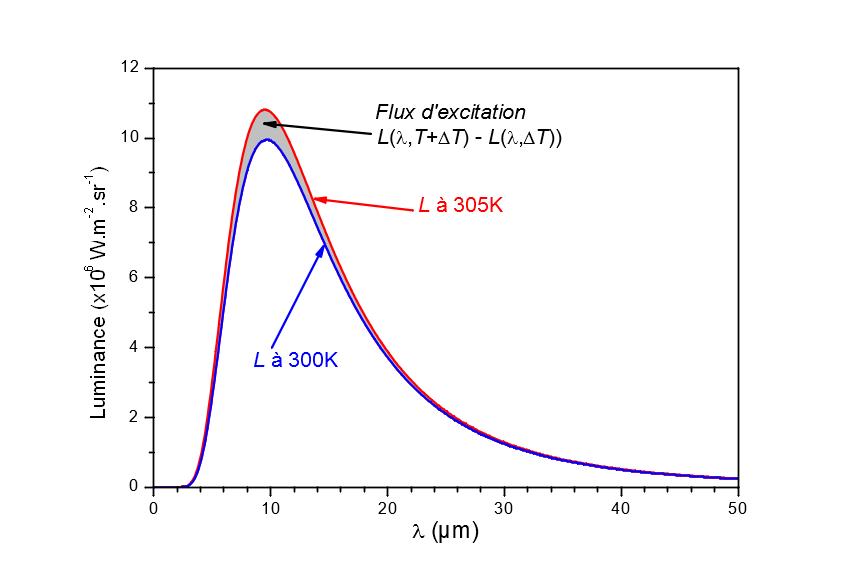
Abbildung 6
Bestimmung der spektralen Verteilung des Anregungsflusses einer modulierten Quelle
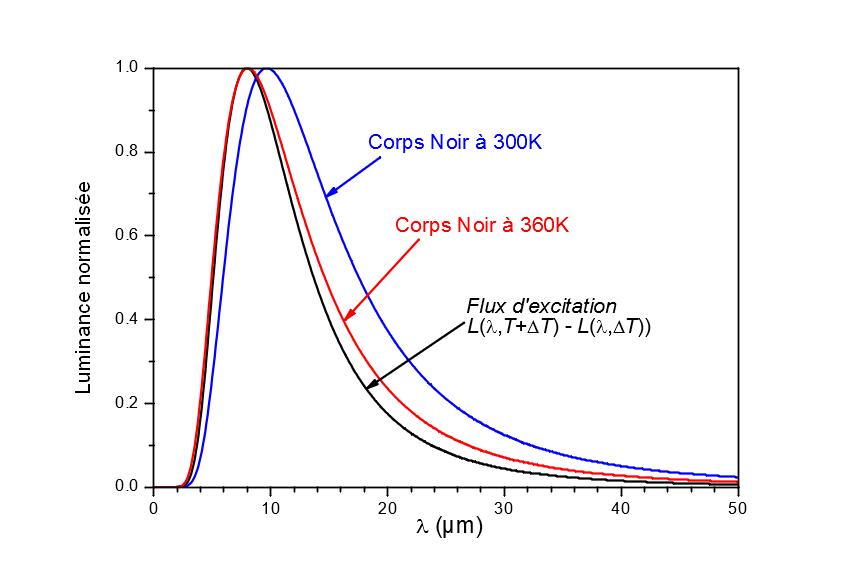
Abbildung 7
Vergleich der spektralen Verteilung des Anregungsflusses einer um 300 K modulierten Quelle mit der eines schwarzen Körpers bei 360 K
Unser Team berät Sie gerne, um Ihren Erwartungen bestmöglich gerecht zu werden.


