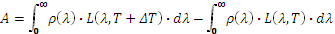Importance et limite des mesures spectrales
Importance et limite des mesures spectrales pour la mesure d’émissivité
Auteurs :
Jean-Pierre MONCHAU, THEMACS Ingénierie, 2bis rue Alfred Nobel, 77420 Champs sur Marne,monchau@themacs.fr
Laurent IBOS, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, ibos@u-pec.fr
Mario MARCHETTI, CEREMA, Laboratoire Régional de Nancy,71, rue de la Grande Haie – 54510 Tomblaine,Mario. Marchetti@cerema.fr
Jean DUMOULIN, IFSTTAR, Dépt. CoSys, Route de Bouaye, 44344 Bouguenais Cedex, jean.dumoulin@ifsttar.fr
Vincent FEUILLET, Université Paris-Est, CERTES/OSU Efluve, 61 avenue du Général De Gaulle, 94010 Créteil Cedex, vincent.feuillet@u-pec.fr
L’émissivité
L’émissivité est une propriété thermophysique des matériaux importante pour quantifier les échanges thermiques par rayonnement. Elle est en outre indispensable pour mesurer la température de surface à partir d’une mesure de luminance comme par exemple par thermographie infrarouge.
Cette dernière technique se généralise avec la démocratisation de caméras thermiques à matrices de micro-bolomètres. La mesure d’émissivité à température ambiante se fait généralement par méthode indirecte en utilisant la loi de Kirchhoff reliant l’émissivité à la réflectance pour un matériau opaque. Plusieurs appareils commerciaux existent, cependant, ces appareils comportent des biais de mesures. Pour corriger ces défauts, il est nécessaire de connaître le comportement spectral du matériau.
La mesure du facteur de réflexion spectrique avec un spectromètre infrarouge à transformée de Fourier (FTIR) muni d’une sphère intégrante permet d’obtenir cette information. La limitation spectrale des sphères intégrantes (généralement 1-20 µm) empêche cependant de se passer d’un émissomètre couvrant un domaine spectral plus large.
Le CERTES a développé un protocole de mesure combinant les deux techniques (large bande et spectrale) pour obtenir une valeur de l’émissivité sans biais, corrigée des variations de la température de la source. Cette méthode a été testée avec succès pour différents matériaux, notamment des céramiques comme l’alumine (Al2O3) présentant de fortes variations de réflectance dans la bande de 1 à 20 µm. Ces résultats sont présentés dans cet article.
Définition de l’émissivité
Max Planck a déterminé théoriquement l’émittance spectrale d’un corps idéal appelé corps noir grâce à la théorie quantique (Figure 1). Les surfaces réelles rayonnent de manière similaire mais l’émittance est pondérée par un coefficient sans dimension appelé émissivité.
Ce coefficient dépend du matériau, de sa température, de la longueur d’onde et de l’incidence (ici l’angle d’émission). Les thermiciens préfèrent utiliser un coefficient intégré sur l’ensemble du spectre et pour l’ensemble des incidences appelé émissivité totale hémisphérique afin de pouvoir par exemple quantifier la quantité de chaleur perdue par rayonnement par une surface.
La difficulté est donc de déterminer ce coefficient sans négliger de longueurs d’onde ou d’incidences.
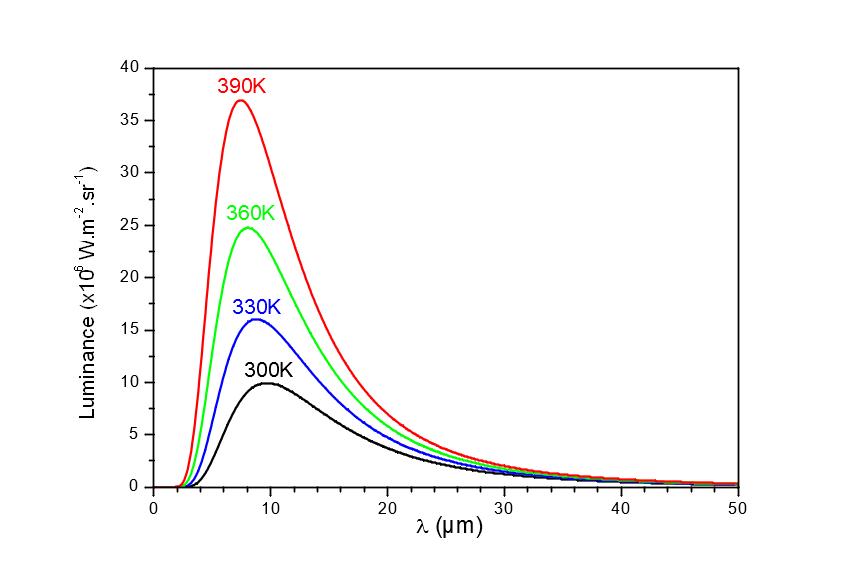
Figure 1
Luminance d’un corps noir L(λ) pour différentes températuresT
Pour mesurer l’émissivité il existe de nombreuses approches que nous pouvons classer en deux catégories : les méthodes directes mesurent le rayonnement énergétique de la surface étudiée et les méthodes indirectes déduisent l’émissivité à partir d’autres propriétés optiques de la surface.
Parmi les méthodes directes, on peut citer la méthode calorimétrique qui consiste à mesurer la puissance électrique à fournir à un échantillon (placé dans un cryostat sous vide) pour maintenir sa température de surface égale à la température à laquelle on souhaite connaître l’émissivité. Le Laboratoire National de Métrologie et d’Essais (LNE) possède un banc de mesure de ce type [3].
Une autre méthode, qualifiée de radiométrique, consiste à mesurer le rayonnement thermique issu de la surface du matériau. Cette mesure peut se faire en fonction de l’angle pour obtenir l’émissivité directionnelle et en fonction de la longueur d’onde (avec un spectromètre FTIR par exemple) pour obtenir l’émissivité spectrale directionnelle. Le dispositif du CEMHTI (Conditions Extrêmes et Matériaux Haute température et Irradiation) permet ce type de mesure à très haute température [4].
Pour la mesure de l’émissivité à température ambiante le niveau du flux est trop faible pour être mesuré avec une bonne précision : c’est le domaine privilégié des méthodes indirectes. Celles-ci utilisent la loi de Kirchhoff reliant l’émissivité ε à la réflectance ρ et à la transmittance τ pour une longueur d’onde λ donnée :
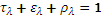
L’émissivité étant égale à l’absorptivité. Pour un matériau opaque, l’émissivité est donc égale à :
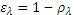
Pour obtenir l’émissivité totale on doit donc sommer le facteur de réflexion spectrique (première fois que je vois ce mot) pondéré par la répartition spectrale énergétique du corps noir à la température à laquelle on souhaite connaitre l’émissivité :
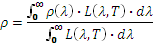
L’autre solution est de mesurer le facteur de réflexion global en éclairant la surface avec une source lumineuse ayant cette répartition énergétique.
Plusieurs dispositifs commerciaux mesurant l’émissivité utilisent cette méthode. Leur principale qualité est de mesurer le facteur de réflexion dans une bande spectrale allant de 1 à 50 µm ce qui représente 95% de l’énergie rayonnée par un corps noir à température ambiante (autour de 300K).Cependant, ils intègrent le facteur de réflexion pour une répartition spectrale différente de la température ambiante.
En effet, ils utilisent comme sources infrarouge des corps noirs ou gris à une température supérieure à la température ambiante. Ces sources ont des répartitions spectrales différentes de celle d’un corps noir à 300 K. Cette différence de répartition spectrale entraîne des erreurs de mesure de l’émissivité pour des corps non gris pouvant aller jusqu’à 5%.Ce défaut n’est pas une nouveauté.
En effet la norme ASTM E408-71 (Standard Test Method for Total Normal Emittance of Surface Using Inspection-Metre Techniques) en fait état. On peut se référer également à [5] où ce type d’erreur est brièvement évoqué.
Les émissomètres développés au CERTES [1,2] utilisent des sources infrarouge modulées en température à des températures très proches de la température ambiante. Le problème reste entier car la modulation affecte notablement la répartition spectrale de la source (voir encadré 1).
Pour lever cette incertitude, il est nécessaire de mesurer le facteur de réflexion spectral directionnel hémisphérique (celui-ci est égal au facteur de réflexion hémisphérique directionnel pour des raisons de réciprocité). Les seuls dispositifs commerciaux permettant de faire cette mesure sont les sphères intégrantes. Elles peuvent être couplées à des spectromètres FTIR et autorisent des mesures dans la bande spectrale 1-20 µm.
Ce qui limite aujourd’hui la bande spectrale des sphères intégrantes commerciales, c’est le revêtement intérieur de celles-ci. Il doit être parfaitement diffusant (comportement lambertien). Ce n’est plus le cas pour des longueurs d’ondes supérieures à 20µm. On doit donc se contenter de cette bande spectrale qui ne représente que 76% de l’énergie rayonné à 300 K.Le dispositif utilisé au CERTES et par THEMACS Ingénierie est un spectromètre infrarouge à transformée de Fourier FRONTIER©de la marque Perkin-Elmer©. Le spectromètre est complété par unesphère intégrante de marque PIKE©.
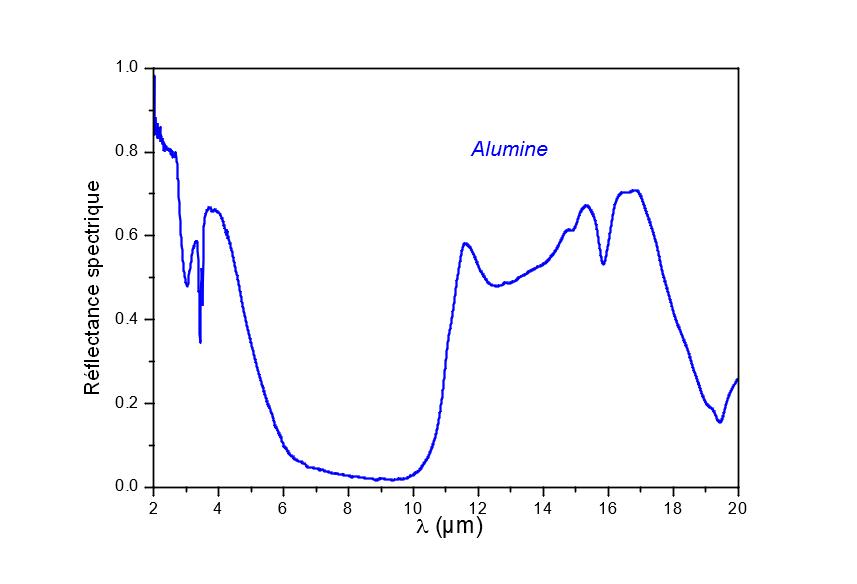
Figure 3
Facteur de réflexion spectrique en fonction de la longueur d’onde d’un échantillon d’alumine
Ces dispositifs expérimentaux sont visibles sur la figure 2. Malgré cette limitation, La mesure spectrale donne des informations exactes sur les variations de l’émissivité en fonction de la température. En combinant les deux techniques (mesure spectrales et mesure en large bande) on peut remonter à une mesure d’émissivité exacte. On peut illustrer cette méthode en étudiant l’alumine (Al2O3) :
Par exemple, dans le cas de l’alumine, l’échantillon utilisé est sous forme de céramique amorphe. Ce type de matériau est un cas d’école car son émissivité spectrale directionnelle varie fortement autour de 10 µm (Figure 3), c’est-à-dire autour du maximum d’émission d’un corps à température ambiante.
C’est fréquemment le cas pour ce type de céramique. En outre les données bibliographiques ne sont pas utilisables. En effet, en fonction de la variété allotropique, du degré de cristallisation, des différents traitements thermiques…, les valeurs de l’émissivité spectrale directionnelle de l’alumine sont très variables [6].
Quand la température de la surface étudiée varie de la température ambiante vers des températures plus élevées, le maximum de luminance de la fonction de Planck L(λ,T) se décale de 10 µm vers les longueurs d’ondes plus courtes.Le maximum de luminance est atteint pour une longueur d’onde λmax(en µm) = 3000/T, avec T en K.
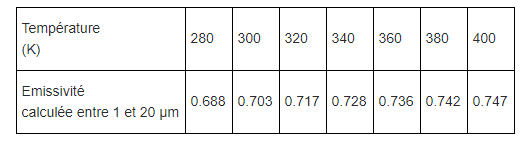
Pour l’alumine, ceci a pour effet de solliciter de manière croissante une région spectrale beaucoup plus émissive. L’émissivité augmente donc avec la température. On peut calculer l’émissivité en prenant en compte seulement la bande spectrale de 1 à 20 µm. Ces données sont présentées dans le tableau 1. Ce calcul néglige une partie importante du spectre utile. La valeur de l’émissivité calculée est ainsi erronée.
Cependant, étant donné le caractère monotone de la fonction de Planck pour des longueurs d’onde supérieures à 20 µm pour cette température, les variations de l’émissivité en fonction de la température ne dépendent donc que de la bande spectrale de 1 à 20 µm. A défaut de connaitre la valeur de l’émissivité, on peut donc en déduire assez précisément le coefficient de variation de l’émissivité en fonction de la température. Si l’on est capable par un autre moyen de mesurer l’émissivité pour une température plus élevéeque la température ambiante, on peut donc en déduire l’émissivité à toutes les températures autour de 300 K.
C’est ce que l’on peut observer sur les graphiques de la figure 4. A partir des mesures spectrales (graphique haut de la figure 4) on peut obtenir les variations d’émissivité en fonction de la température (graphique de bas de la figure 4, tracé bleu). L’émissomètre EM2 du CERTES [2] (figure 5) permet d’obtenir une valeur sans biais de l’émissivité mais seulement à 360K. A partir de ces deux informations on remonte à l’émissivité sans biais en fonction de la température (graphique de bas de la figure 4, tracé rouge).
Figure 4
Réflectance spectrique de l’alumine, en haut; calcul de l’émissivité à partir des mesures spectrales et d’un émissomètre large bande (EM2 [2]), en bas.
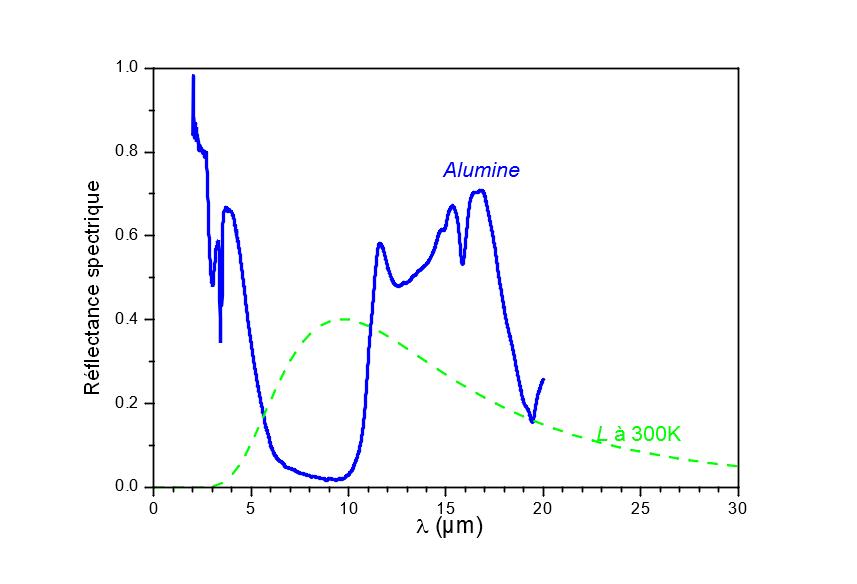
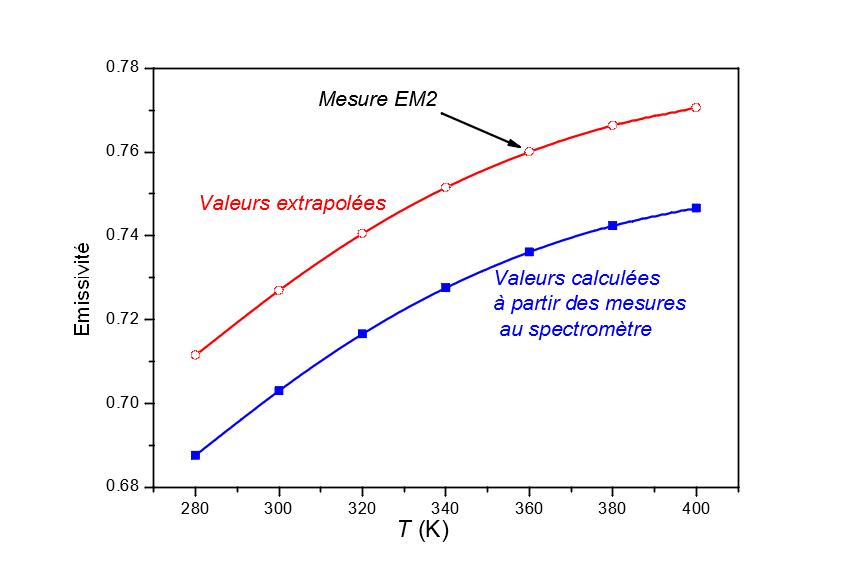

Figure 5
Emissomètre EM2, développé au CERTES Breveté en 2012 (FR 2987121)
Conclusion
La mesure des propriétés spectrales des surfaces dans le domaine de l’infrarouge est indispensable pour connaître le comportement radiatif de ces surfaces. La seule mesure de l’émissivité avec un appareil commercial ne permet pas d’atteindre une valeur exacte de l’émissivité. La plupart de ces appareil commerciaux ont été conçus pour du contrôle en production, pas pour obtenir une valeur de l’émissivité directionnelle.
La combinaison des deux méthodes de mesure et une bonne connaissance des caractéristiques des appareils utilisés permettent d’obtenir des mesures exemptes d’erreurs systématiques.
La numérotation ne correspond pas à l’ordre d’apparition dans le document
- L. Ibos, M. Marchetti, A. Boudenne, S. Datcu, J.Livet, Y. Candau, Infraredemissivitymeasurementdevice:
Principle and applications, Meas. Sci. Technology.17, 2950 (2006) - J-P. Monchau, M. Marchetti, L. Ibos, J. Dumoulin, V. Feuillet, Y. Candau, Infrared Emissivity Measurements of Building and Civil Engineering Materials: A New Device for Measuring Emissivity,Int. J. Thermophys., in press
- J. Hameury, B. Hay, J. R. Filtz, Measurement of Total Hemispherical Emissivity Using a Calorimetric
Technique, Int. J. Thermophys, 28, 1607 (2007) - O. Rozenbaum, D. De Sousa Meneses, Y. Auger, S. Chermanne and P. Echegut, A spectroscopic method to
measure the spectral emissivity of semi-transparent materials up to high temperature, Rev. Sci. Instrum. 70, 4020 (1999) - K.E. Nelson, E.E.Leudke, J.T.Bevans, A device for rapid measurement of total emittance, Journal of
Spacecraft and Rockets, 3, 758 (1966) - Thermophysical Properties of High Temperature Solid Materials, Vol. 4, Y. S. Touloukian Editor
Encadre
Erreurs dues à la modulation de température de la source
Ce cas de figure concerne les méthodes utilisant une méthode réflectométrique impliquant une source modulée. On suppose que la répartition spectrale de la source ne varie pas de manière notable quand les variations de température sont faibles. Cette hypothèse est exacte, cependant avec ces méthodes, on ne mesure pas le flux réfléchi par l’échantillon mais seulement les variations de flux réfléchi.
Cela s’applique aussi pour les sources hachées par un écran mobile (chopper). En effet, dans ce cas, on mesure l’alternance entre la température de la source et celle de l’écran. Si la température T est une fonction périodique du temps, il faut considérer son expression en fonction du temps T(t) où t est le temps. Le signal mesuré par le détecteur est donc égal à:
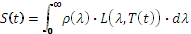
où L(λ,T) est la luminance du corps noir pour la longueur d’onde λ à la température T. Cette différence est illustrée sur la figure 6.
Puisque l’on ne s’intéresse dans ce cas qu’aux variations périodiques de cette luminance, la mesure est donc proportionnelle à l’amplitude crête à crête notée A mesurée par le détecteur pour des variations de température ΔT au-dessus de la température minimale (pour des raisons de simplification d’écriture, on suppose que la température varie entre T et T+ΔT):
Si l’on mesure le signal correspondant au flux incident, on peut obtenir le coefficient de réflexion total dans la bande spectrale couverte par le détecteur:
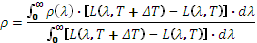
On voit donc qu’en réalité, on mesure la réflectance avec une source ayant une répartition spectrale égale à la différence de luminance de deux sources de températures différentes. Cette répartition spectrale diffère notablement de la répartition spectrale d’un corps noir à la température moyenne.
La figure 7 montre la luminance d’un corps noir à 300 K et à 360 K ainsi que la différence de luminance entre deux corps noirs à 300 K et 305 K. Les courbes ont été normalisées pour faciliter la lecture. On remarque que la répartition spectrale de la source modulée ne suit plus la loi de Planck, mais se rapproche de la répartition spectrale d’un corps noir à 360 K. Pour que cette erreur n’ait qu’une influence négligeable, il faut que l’échantillon puisse être assimilable à un corpsgris aux alentours de 10 µm ou connaître les propriétés spectrales dela surface étudiée.
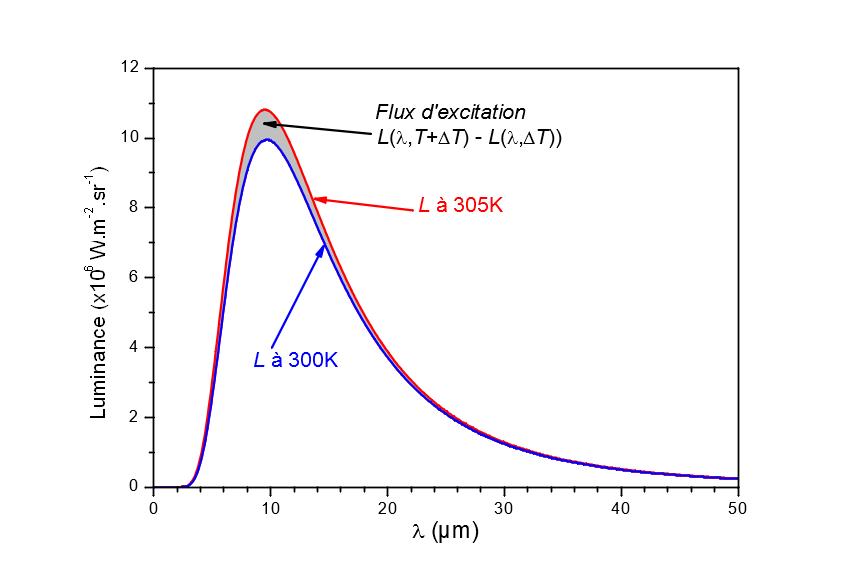
Figure 6
Détermination de la répartition spectrale du flux d’excitation d’une source modulée
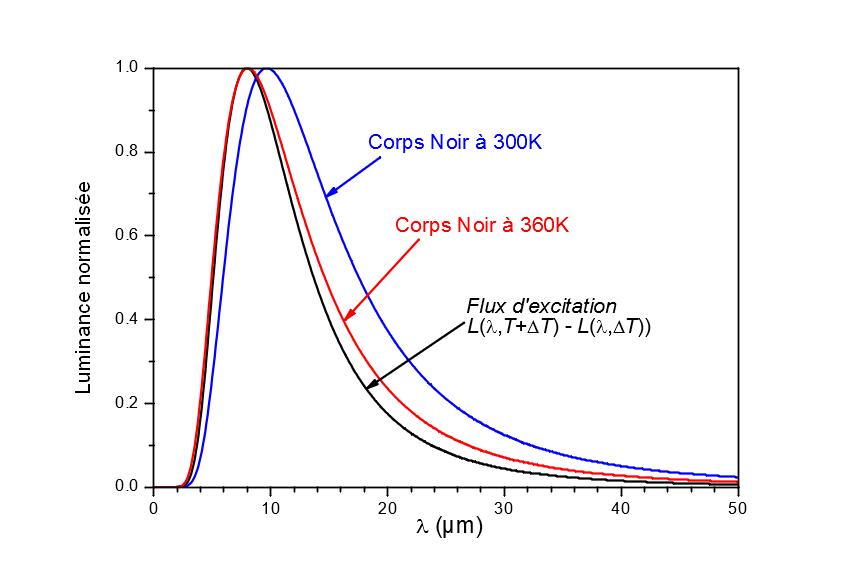
Figure 7
Comparaison de la répartition spectrale du flux d’excitation d’une source modulée autour de 300 K à celle d’un corps noir à 360 K
Notre équipe vous conseille pour répondre au mieux à vos attentes